4.3. Trapecios
Para dibujar cualquier trapecio tienes que aplicar los procedimientos seguidos en la construcción de triángulos (isósceles, escaleno o rectángulos).
Además de las propiedades mencionadas en el apartado anterior (3.1) en todos los trapecios se dan las siguientes relaciones:
TRAPECIO ESCALENO: Además de las propiedades mencionadas en el apartado anterior (3.1) en un trapecio escaleno se dan las siguientes relaciones:
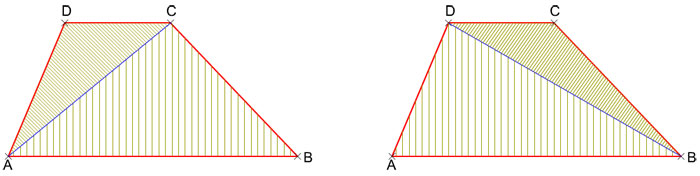
- La diagonal mayor o menor lo descompone en dos triángulos escalenos obtusángulos.

CONSTRUCCIÓN:
Método Directo:
- Conocida su base mayor en verdadera magnitud y posición, un lado no paralelo, el ángulo que forma con la base mayor y la longitud de la otra base:
- Dada su base mayor en verdadera magnitud y posición, la altura y la longitud de los lados no paralelos:
Método de los lugares geométricos:
- Conocida su base mayor en verdadera magnitud y posición, la longitud de la otra base y los lados no paralelos:
- Dada su base mayor en verdadera magnitud y posición, la longitud de la otra base y la longitud de las dos diagonales:
TRAPECIO ISÓSCELES: Además de las propiedades mencionadas en el apartado anterior (3.1) en un trapecio isósceles se dan las siguientes relaciones:
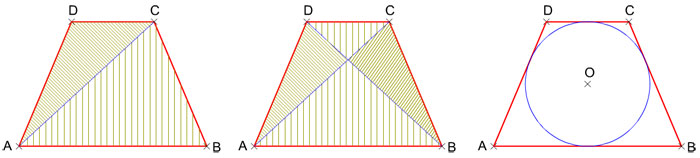
- Una diagonal lo descompone en dos triángulos escalenos: uno obtusángulo y otro acutángulo.
- Las dos diagonales lo descomponen en cuatro triángulos: dos isósceles desiguales y dos escalenos iguales (que pueden ser rectángulos).
- El radio de la circunferencia inscrita es igual a la mitad de la longitud de la altura.

CONSTRUCCIÓN:
Método Directo:
- Conocida base mayor en verdadera magnitud y posición, la longitud de la otra base y la altura:
- Dada la base mayor en verdadera magnitud y posición, los ángulos interiores adyacentes y la longitud de una de sus diagonales:
Método de los lugares geométricos:
- Dada su base mayor en verdadera magnitud y posición, su altura y el ángulo que forman las diagonales entre sí:
- Conocida la base mayor en verdadera magnitud y el radio de la circunferencia inscrita:
TRAPECIO RECTÁNGULO: Además de las propiedades mencionadas en el apartado anterior (3.1) en un trapecio rectángulo se dan las siguientes relaciones:
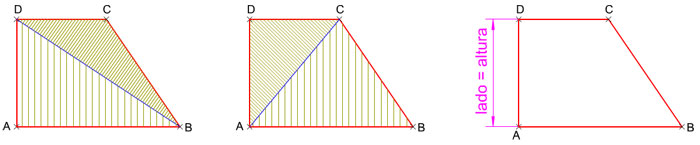
- La diagonal mayor o menor lo descompone en dos triángulos: uno rectángulo escaleno y otro obtusángulo (isósceles o escaleno).
- La longitud de la altura coincide con la longitud del lado menor no paralelo.

CONSTRUCCIÓN:
Método Directo:
- Conocida base mayor en verdadera magnitud y posición, la longitud de la otra base y la altura:
- Dada la base mayor en verdadera magnitud y posición, la altura y la longitud del lado oblicuo:
- Conocida su altura en verdadera magnitud y posición y las longitudes de las diagonales:
Método de los lugares geométricos:
- Dada la suma de la base mayor y la altura en verdadera magnitud y posición, y las longitudes de las diagonales:
- Conocida la resta entre la base mayor y la altura en verdadera magnitud y posición y las longitudes de la base menor y de la diagonal mayor:
Elige la opción que tú creas más adecuada
Todos los trapecios isósceles tienen circunferencia inscrita
Verdadero Falso