6.1. Ciclo de Carnot

En el siglo XIX el ingeniero francés Nicolas Carnot concibió, estudió y desarrolló un ciclo termodinámico, que constituye el ciclo básico de todos los motores térmicos, en el:
  • Se suministra al motor energía en forma de calor a temperatura elevada.
  • La acción del calor permite realizar un trabajo mecánico al motor.
  • El motor cede calor al foco de temperatura inferior.

El ciclo de Carnot es un ciclo teórico y reversible, su limitación es la capacidad que posee un sistema para convertir en calor el trabajo, se utiliza en las máquinas que usan vapor o una mezcla de combustible con aire u oxígeno.

Icono IDevice Actividad
Se dice que un proceso termodinámico es reversible, cuando acometiendo pequeños cambios en el ambiente podemos conseguir que recorra su trayectoria inversa. En la práctica es imposible, en la naturaleza todos los procesos que ocurren son irreversibles. Sin embargo el estudio de estos procesos es muy útil pues nos da el valor del rendimiento máximo que se puede obtener de una máquina.

Representado en un diagrama p-v se obtiene la siguente figura:
Imagen 14. periodni. Copyright

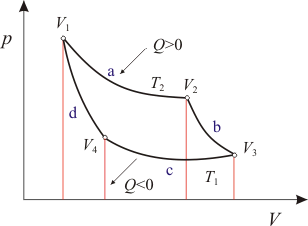
El ciclo se divide en cuatro etapas, cada una de las cuales se corresponde con una transformación termodinámica básica:

  • Etapa A) Expansión isotérmica

En el gráfico es el paso del estado 1 al estado 2. Es un proceso isotermo y por ser un gas perfecto eso hace que la temperatura se mantenga constante T1.

El gas se encuentra en un estado de equilibrio inicial representado por p1, V1, T1, en el interior del cilindro. Se produce una expansión isotérmica entre 1 y 2, hasta alcanzar los valores p2, V2, T1, el sistema realiza un trabajo W1 positivo (aumenta el volumen, luego es un trabajo hecho por el sistema, trabajo positivo), comunicando energía al entorno, por otro lado como la variación de energía interna ha de ser cero, toma un calor del entorno equivalente Q1:

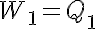
  • Etapa B) Expansión adiabática

Se parte del punto 2 y se llega al estado 3.

Por ser un proceso adiabático no hay transferencia de calor, el gas debe realizar un trabajo, elevando el émbolo, para lo que el cilindro debe estar aislado térmicamente, alcanzándose los valores p3, V3, T2.

  • Etapa C) Compresión isotérmica

Entre los estados 3 y 4, hasta alcanzar los valores p4, V4, T2, siendo el trabajo realizado por el pistón. En este caso es un trabajo de compresión (negativo), se recibe energía del entorno en forma de trabajo y se cede una energía equivalente en forma de calor:

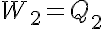
  • Etapa D) Compresión adiabática

Entre los estados 4 y 1 cerrándose el ciclo.

Se alcanzan de nuevo los valores p1, V1, T1 sin transferencia de calor con el exterior.

Consideramos ahora el efecto global del ciclo.

  • El trabajo neto W realizado durante el ciclo por el sistema será el representado por la superficie encerrada en el trayecto 1-2-3-4-1.
  • La cantidad neta de energía calorífica recibida por el sistema será la diferencia entre Q2 y Q1.

Para calcular el rendimiento de un ciclo de Carnot se emplea la misma expresión mencionada anteriormente:

 


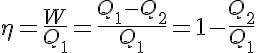
En la práctica es mucho más difícil obtener los valores de los calores trasegados que los valores de la temperatura (en grados Kelvin) de los dos focos, que se conocen por la lectura de un termómetro, y se puede considerar que la transmisión de calor es proporcional a las temperaturas de ambos focos sin que se cometa un error apreciable (recuerda que son gases perfectos y que la variación de energía interna es fución exclusiva de la variación de temperatura) por lo que se puede escribir:

 


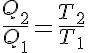
Y por lo tanto se puede expresar el rendimiento como:

 


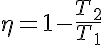
El rendimiento de este tipo de máquinas será mayor cuanto mayor sea la diferencia entre las temperaturas del foco caliente T1 y el foco frío T2.

Existen otros ciclos termodinámicos que también poseen el rendimiento máximo aunque se utilizan mucho menos que el de Carnot.

 

Icono de iDevice Caso de estudio
Los siguientes ejercicios hacen referencia al rendimiento máximo teórico que se puede obtener de una máquina térmica.
Una máquina térmica reversible con un rendimiento del 30% y cuyo foco frío se encuentra a 107ºC, cede una cantidad de calor de 120 kcal a dicho foco frío durante cada ciclo. Determina la temperatura y el calor cedido por el foco caliente.

Una máquina térmica se encuentra funcionando entre dos focos a 27ºC y a 227ºC y tiene un rendimiento del 25% del máximo posible. Se repite el ciclo con una frecuencia de 5 veces cada segundo, siendo su potencia 20 kW. Determina el trabajo que se produce en cada ciclo y cuántas kcal/hora cede al foco frío.

Para mantener una temperatura en su interior de -18ºC un congelador funciona con un COP real de 1/3 de su valor teórico máximo, para ello consume una potencia de 2kw. Si consideramos que la temperatura ambiental permanece a 20ºC. Determina la energía que se tiene que extraer del congelador.

Una máquina térmica trabaja entre dos focos a 300 ºC y 100 ºC. Absorbiendo una cantidad de calor Q1 = 100 Kcal y cediendo un trabajo de 50.KJ.
Determinar:
a) El rendimiento de la máquina térmica.
b) El máximo rendimiento que podría llegar a tener esa máquina térmica.
c) El calor cedido a la fuente fría.

Una máquina térmica absorbe 900 J de un foco caliente que se encuentra a 177ºC, presentando una eficiencia del 40%.
Determina:

a) Calor cedido al foco frío

b) Temperatura a que se encuentra el foco frío.


Icono de iDevice Caso de estudio
CICLO DE CARNOT

Un gas ideal diatómico (cv=5/2 R) se encuentra inicialmente a una temperatura T1=27ºC, una presión p1=105 Pa y ocupa un volumen V1=0.4 m3. El gas se expande adiabáticamente hasta ocupar un volumen V2=1,2 m3. Posteriormente se comprime isotérmicamente hasta que su volumen es otra vez V1 y por último vuelve a su estado inicial mediante una transformación isócora. Todas las transformaciones son reversibles.

a) Dibuja el ciclo en un diagrama p-V. Calcula el número de moles del gas y la presión y la temperatura después de la expansión adiabática.
b) Calcula la variación de energía interna, el trabajo y el calor en cada transformación.


Un frigorífico que actúa según un ciclo de Carnot, funciona con 18 moles de un gas ideal monoatómico, realizando ciclos de 2 s de duración. Las temperaturas de los focos son 450 K y 150 K y consumiendo una potencia de 60 kW.
Se pide:
a) Dibuja el ciclo en un diagrama p-V especificando las transformaciones que lo componen. Calcula la eficiencia.
b) Calcula el calor intercambiado en cada etapa y la relación entre los volúmenes en la compresión isoterma.
c) Sabiendo que después de la expansión isoterma el volumen del gas es V3= 0.5 m3, calcula la presión y el volumen después de la compresión adiabática.

« Anterior | Siguiente »