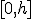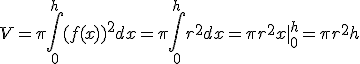1.1. Técnica integral de capacidades
|
|
| Sólidos de revolución. Animación del Banco de imágenes del ITE. |
Una de las aplicaciones que va a tener la integral es el cálculo de volúmenes de sólidos de revolución. Estos sólidos son los que se generan al girar la gráfica de una función alrededor del eje de abscisas. En la ventana interactiva de la derecha puedes observar algunos de estos sólidos de revolución.
Pero, ¿cómo podemos calcular el volumen de estos sólidos de revolución? Pulsando sobre la ventana interactiva que aparece más abajo podrás observar paso a paso la forma de hacerlo.
|
|
 |
| Tubo de escape. Imagen obtenida del Banco de imágenes del ITE. |
Los sistemas con los que más cuidado deben tener en la empresa GP Association que observaste en la historia inicial son aquellos asociados al motor del coche. En este caso nos vamos a ocupar del tubo de escape. Los diseñadores de la empresa han realizado un dibujo provisional de la mitad del perfil de este tubo de escape. Esta mitad se adapta a la función
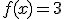 en el intervalo
en el intervalo 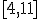 .
.
El tubo de escape se genera al rotar esta función alrededor del eje de abscisas. Este es el tubo ideal para lograr que el coche pueda reducir su espacio con un mecanismo que han situado en una zona cercana a ese tubo. Pero además, el tubo de escape debe cumplir las normas de reducción del ruido, por lo que su volumen debe ser superior a 150.
 y de altura
y de altura 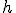 .
.
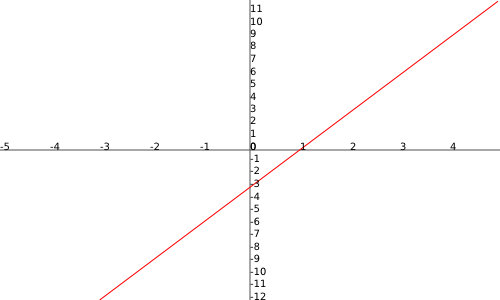
Ahora te proponemos calcular el volumen de otro de los sólidos de revolución: el cono, que puedes contemplar en la ventana interactiva que aparece más abajo. Para ello, vamos a obtener el cono como el sólido que se obtiene al girar una recta secante con el eje de abcisas alrededor de este eje. En este caso, la recta que vamos a hacer girar es la función:
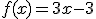
Que aparece representada en rojo en la imagen siguiente.
 |
Y te pedimos:
a) que calcules el volumen del cono que resulta de girar esta recta alrededor del eje de abcisas en el intervalo 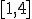 .
.
b) que calcules el volumen del cono que resulta de girar esta recta alrededor del eje de abcisas en el intervalo 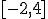 .
.
El volumen pedido en el apartado a) es: ,47 u.v.
El volumen pedido en el apartado b) es: u.v.
Para profundizar en el cálculo de volúmenes de cuerpos como aplicación de la integral puedes observar un desarrollo más completo de este estudio en la siguiente ventana. Pulsa sobre ella para ir avanzando poco a poco.


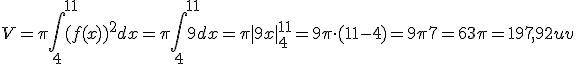
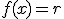 alrededor del eje de abacisas en el intervalo
alrededor del eje de abacisas en el intervalo