1.3. ¿Cuándo funciona la derivada?
La derivada de una función en un punto lleva a otro concepto que es el de derivabilidad. Si tenemos un función  diremos que es derivable en un punto
diremos que es derivable en un punto 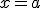 si existe la derivada de la función en ese punto. Es más, diremos que la función es derivable en un intervalo
si existe la derivada de la función en ese punto. Es más, diremos que la función es derivable en un intervalo 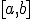 si es derivable en todos los puntos interiores de ese intervalo y, además, a la derecha de a y a la izquierda de b.
si es derivable en todos los puntos interiores de ese intervalo y, además, a la derecha de a y a la izquierda de b.
Diremos que vamos a estudiar la derivabilidad de una función cuando vamos a calcular todos los valores en los que la función es derivable.
 |
| Cohete. Imagen obtenida del Banco de imágenes del ITE. |
La agencia espacial europea le ha presentado a la empresa de Ángela y Andrés un prototipo de cohete que desean fabricar. Les han pedido que estudien el rozamiento que el cohete puede tener con el aire en el momento de entrar en la atmósfera terrestre. La agencia espacial sabe que en ese momento crítico es cuando el morro del cohete va a soportar más presión.
Andrés y Ángela, que ya han realizado varios estudios de este tipo, saben que ese rozamiento va a depender de la derivabilidad en cada uno de los puntos de la función que describe el perfil del morro del cohete. Han estudiado este perfil y saben que se ajusta perfectamente a la función 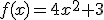 , por lo que, para comenzar su estudio deben investigar la derivabilidad de esta función y ver los puntos en los que no es derivable. Ayúdales a realizar este estudio.
, por lo que, para comenzar su estudio deben investigar la derivabilidad de esta función y ver los puntos en los que no es derivable. Ayúdales a realizar este estudio.
Si una función  es derivable en un punto
es derivable en un punto 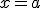 , entonces la función es continua en ese punto también.
, entonces la función es continua en ese punto también.
Esta propiedad tiene una sencilla demostración que puedes observar en el siguiente enlace.
Estudia la continuidad y la derivabilidad de la siguiente función en el punto x=0:
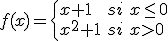
Si tenemos la función
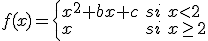
Calcula los valores de 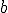 y de
y de  para que la función sea derivable en
para que la función sea derivable en 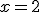 .
.
Ayuda: debes imponer las condiciones para que la función sea continua y derivable y te saldrá un sistema de dos ecuaciones con las incógnitas b y c.
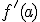 .
.
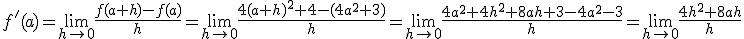
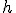 tenemos que:
tenemos que:
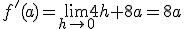
 , por tanto la función anterior es derivable en todos los valores reales, es decir, es derivable en el intervalo
, por tanto la función anterior es derivable en todos los valores reales, es decir, es derivable en el intervalo 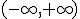
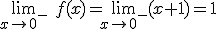
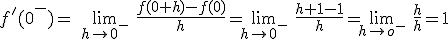
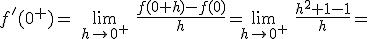
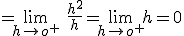
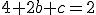 , de donde, despejando obtenemos
, de donde, despejando obtenemos 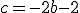 .
. 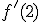 los límites laterales deben coincidir, llegamos a que
los límites laterales deben coincidir, llegamos a que 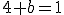 y por tanto
y por tanto 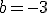 .
. 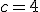 .
.