1.1. Del valor medio al instantáneo
 |
| Carrera de motos. Imagen obtenida del Banco de imágenes del ITE. |
¿Has visto alguna vez una carrera de motos? Todos parten de condiciones más o menos iguales. La velocidad de partida es cero, el lugar de partida es casi el mismo, el carburante utilizado es el mismo... y todos parten al mismo tiempo. Pero al final la llegada de cada uno no es la misma. Unos llegan antes que otros. ¿Qué ha pasado a lo largo de la carrera? Si hiciéramos una foto del desarrollo en un momento dado, obtendríamos algo parecido a lo que observamos en la imagen de la derecha. Al final de la carrera cuenta el resultado, la posición en la que se ha llegado. Pero esa posición es fruto de los distintos instantes que componen la carrera. Adelantamientos, aceleración, frenada en las curvas.... Con las funciones sucede algo parecido. Vamos a estudiarlo en profundidad fijándonos en un ejemplo.
Consideramos la función 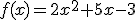 .
.
Si queremos estudiar la tasa de variación media de la función entre dos puntos  y
y 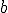 realizaríamos la operación
realizaríamos la operación
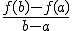 por ejemplo, la tasa de variación media de la función entre 2 y 5 sería:
por ejemplo, la tasa de variación media de la función entre 2 y 5 sería:
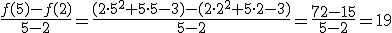
Así, tenemos claro lo que sucede y cómo debemos actuar para calcular la tasa de variación media de la función entre dos puntos pero, ¿Cómo lo hacemos para un instante dado? Por ejemplo, con la función que tenemos ¿Qué pasa en el instante 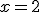 ? Consideremos los siguientes valores:
? Consideremos los siguientes valores:
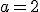 y
y 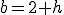 . La tasa de variación media de la función entre estos dos puntos sería:
. La tasa de variación media de la función entre estos dos puntos sería:
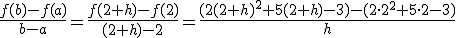
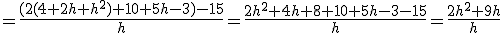
Si nos aproximamos con 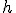 a cero, nos acercaríamos a calcular la tasa de variación de la función en el punto
a cero, nos acercaríamos a calcular la tasa de variación de la función en el punto 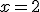 o lo que es lo mismo, nos acercaríamos a calcular la tasa de variación instantánea en
o lo que es lo mismo, nos acercaríamos a calcular la tasa de variación instantánea en 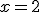 . Así, en nuestro ejemplo, para acercarnos al valor de la tasa de variación instantánea en el 2, vamos a aproximar
. Así, en nuestro ejemplo, para acercarnos al valor de la tasa de variación instantánea en el 2, vamos a aproximar 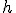 a cero. Esta aproximación la hacemos con el límite:
a cero. Esta aproximación la hacemos con el límite:
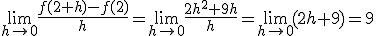
Y así tendríamos la tasa de variación instantánea en 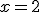 .
.
Observa el recorrido que hemos hecho con el ejemplo y comprueba que coincide con la siguiente definición:
Si tenemos una función  , la tasa de variación media de la función entre dos puntos
, la tasa de variación media de la función entre dos puntos  y
y 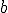 viene dada por:
viene dada por:
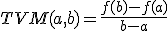
De la misma forma, la tasa de variación instantánea en un punto  viene dada por:
viene dada por:
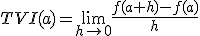
Unos diseñadores informáticos han estado trabajando durante varios meses para poder acercar, a través de Internet, una visita a la Capilla Sistina. Más abajo puedes observar el resultado obtenido. Como puedes comprobar, te puedes mover por toda la capilla para observar cada uno de los detalles que aparecen. El movimiento que se puede realizar en cada una de las direcciones lo han conseguido a través de una función plana que se aplica en la dirección en la que se mueve el ratón del ordenador, de forma que pueda seguir ofreciendo una perspectiva próxima a la realidad. La función utilizada es:
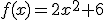
De esta función han realizado las siguientes anotaciones en su estudio:
1.- La tasa de variación media entre los valores 1 y 3 es .
2.- La tasa de variación media entre los valores 4 y 8 es .
3.- La tasa de variación instantánea en el valor 3 es .
4.- La tasa de variación instantánea en el valor 5 es .
Ayúdales completando los valores.