1.2. ¿Qué es la derivada?
 llamamos derivada de la función en un punto
llamamos derivada de la función en un punto 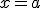 a la tasa de variación instantánea de la función en el punto
a la tasa de variación instantánea de la función en el punto  y se denota
y se denota 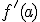 . Así, según la definición tenemos que:
. Así, según la definición tenemos que:
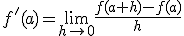
Recuerda que para que exista este límite, deben existir los límites laterales y coincidir. Así, de la misma forma, podemos definir las derivadas laterales como:
.- Derivada por la derecha:
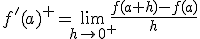
.- Derivada por la izquierda:
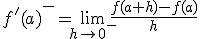
 |
| Motor. Imagen obtenida del Banco de imágenes del ITE. |
La empresa de motores MOTORESA ha diseñado un nuevo motor de gasolina que pretende introducir en el mercado. Los ingenieros de la empresa saben que el consumo de gasolina depende de la velocidad a la que vaya el motor. Si llamamos 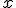 a la velocidad, la función que proporciona el consumo de gasolina en función de la velocidad es
a la velocidad, la función que proporciona el consumo de gasolina en función de la velocidad es
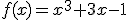
Para contrastar lo bueno que es el motor frente a sus competidores, han decidido basarse en la tasa de variación instantánea del consumo del motor a velocidad 1.
Calcula esa tasa de variación instantánea.
1.- 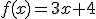
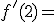
2.- 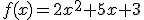
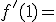
3.- 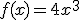
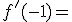
Si tenemos la función
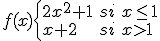
Comprueba si la función es derivable en 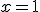 . Reflexiona sobre el comportamiento de la derivada en ese punto.
. Reflexiona sobre el comportamiento de la derivada en ese punto.