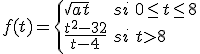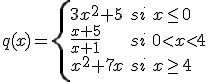2.2 Ejemplos prácticos de paradas

Estudio. Imagen obtenida del Banco de Imágenes del ITE.

Ahora ya conoces todo respecto a la continuidad de funciones, solamente te queda practicar.

Debes tener presente una cosa, cuando necesites estudiar la continuidad de una determinada función, además de indicar los puntos en los que es continua, también debes indicar el tipo de discontinuidad que presenta en los que no es continua.

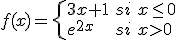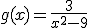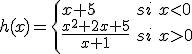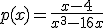Icono de iDevice AV - Actividad de Espacios en Blanco
Ahora te proponemos que estudies la continuidad de las siguientes funciones y, una vez que lo hayas hecho completes los huecos que aparecen más abajo teniendo en cuenta que ninguna de las afirmaciones se repite:



q(x) presenta una discontinuidad en x= .

presenta una discontinuidad en x=3.

es continua para todos los valores.

presenta una discontinuidad en x=0.

presenta una discontinuidad en x=4

g(x) presenta una discontinuidad en x= .

presenta una discontinuidad de salto infinito en x=0

 

Posteriormente puedes comprobar la investigación realizada utilizando la siguiente ventana para representar las gráficas completas o alguna de sus partes.

 

  

Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí

Icono de iDevice Ejemplo o ejercicio resuelto

La empresa TESTUDIO está realizando un trabajo especial para observar el rendimiento de los motores diesel de un determinado modelo de automóvil. En su estudio ha detectado que la gráfica de dicho rendimiento es la siguiente:

 

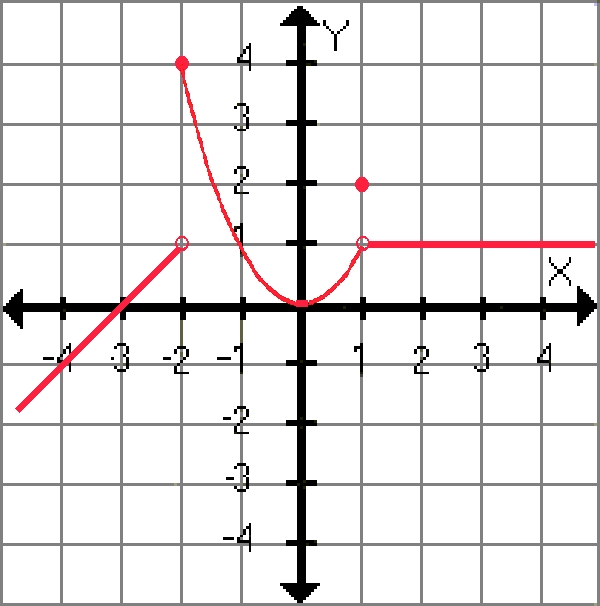Estudia la continuidad de la misma.


Icono de iDevice AV - Actividad de Espacios en Blanco

Sabemos que el movimiento que realiza un brazo mecánico en función del tiempo transcurrido 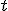viene marcado por la siguiente función:

 

Evidentemente, ese movimiento debe ser continuo a lo largo de todo el tiempo . Para que así sea sabemos que a=
  

« Anterior | Siguiente »