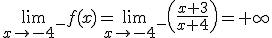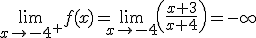2.1. Posibles averías
El primer tipo de discontinuidad que vamos a definir es la discontinuidad evitable.
Si tenemos una función 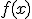 , decimos que presenta una discontinuidad evitable en el punto
, decimos que presenta una discontinuidad evitable en el punto 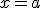 cuando ocurre alguna de las siguientes cosas:
cuando ocurre alguna de las siguientes cosas:
1.- Existe 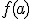 y existe
y existe 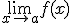 pero son distintos. (cuando decimos que existe el límite, nos referimos a que ese límite es un número)
pero son distintos. (cuando decimos que existe el límite, nos referimos a que ese límite es un número)
2.- No existe 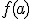 , pero existe
, pero existe 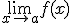
En este caso diremos que 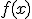 presenta una discontinuidad evitable en el punto
presenta una discontinuidad evitable en el punto 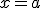 . Se llama así ya que esta discontinuidad la podemos evitar definiendo
. Se llama así ya que esta discontinuidad la podemos evitar definiendo 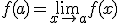
Si tenemos la función
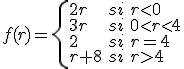
Comprueba que en 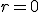 y en
y en 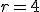 presenta una discontinuidad de tipo evitable
presenta una discontinuidad de tipo evitable
Otro tipo de discontinuidad que se puede presentar es no evitable. Si tenemos una función 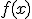 , diremos que presenta una discontinuidad no evitable de primera especie cuando
, diremos que presenta una discontinuidad no evitable de primera especie cuando
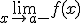 es distinto del
es distinto del 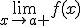 . Es decir, cuando los límites laterales son distintos. Podemos distinguir dos casos:
. Es decir, cuando los límites laterales son distintos. Podemos distinguir dos casos:
a) Si uno o los dos límites laterales son infinitos, la discontinuidad se llama de salto infinito.
b) Si los dos límites laterales son finitos, pero distintos, la discontinuidad se llama de salto finito.
Consideremos ahora la función
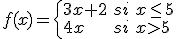
Comprueba que presenta una discontinuidad de salto finito en 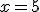
Consideremos la función
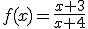
Estudia la o las discontinuidades que presenta.
Represéntala en la pantalla que aparece más abajo y comprueba que los resultados obtenidos son ciertos
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
 |
| Salpicadero. Imagen obtenida del Banco de Imágenes del ITE. |
Los ingenieros de CITRENFOR han diseñado una nueva aplicación para el control de estabilidad de los coches que fabrican. La aplicación va a ir integrada en un pequeño chip que mejorará considerablemente el control de estabilidad.
La aplicación se basa en una función que, dependiendo de la altura en centímetros a la que se encuentre el lateral izquierdo del coche respecto al eje de las ruedas delanteras, corregirá la trayectoria de las ruedas. La función que rige todo este control de estabilidad es:
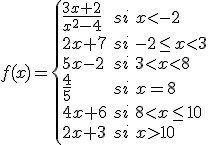
Los ingenieros quieren identificar problemas que ya tienen estipulados en un manual. Así, sabemos que:
.- Si en un punto de una función se presenta una discontinuidad evitable, según el manual que han elaborado, el error es el 834.
.- Si en un punto de una función se presenta una discontinuidad no evitable de salto finito, según el manual que han elaborado, el error es el 848.
.- Si en un punto de una función se presenta una discontinuidad no evitable de salto infinito, según el manual que han elaborado, el error es el 890.
.- Si en un punto de una función no se presenta ningún tipo de discontinuidad, según el manual que han elaborado, el error es el 000 (no existe error)
Teniendo en cuenta esto, podemos decir que:
.- En 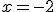 se presenta el error
.
se presenta el error
.
.- En 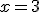 se presenta el error
.
se presenta el error
.
.- En 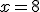 se presenta el error
.
se presenta el error
.
.- En 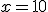 se presenta el error
.
se presenta el error
.
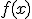 cuando no existe alguno de los límites laterales o no existen ambos límites. Un ejemplo de este tipo de discontinuidad lo encontramos en la función
cuando no existe alguno de los límites laterales o no existen ambos límites. Un ejemplo de este tipo de discontinuidad lo encontramos en la función 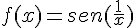 cuya representación gráfica observamos en la ventana inferior. Amplia la imagen acercándote al orígen de coordenadas y observa la gráfica de al función. Así comprenderás el motivo por el que no existen los límites laterales de esta función.
cuya representación gráfica observamos en la ventana inferior. Amplia la imagen acercándote al orígen de coordenadas y observa la gráfica de al función. Así comprenderás el motivo por el que no existen los límites laterales de esta función.
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
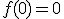 y
y 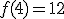 para que la función obtenida fuese continua en todo su dominio.
para que la función obtenida fuese continua en todo su dominio.
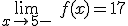 y
y 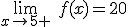 . Por lo tanto hay una discontinuidad de salto finito.
. Por lo tanto hay una discontinuidad de salto finito.
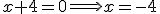
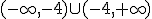 o lo que es lo mismo
o lo que es lo mismo 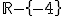 .
.
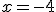 .
.
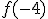 , que no existe ya que
, que no existe ya que