1.2. ¿Cuándo se puede detener un coche?
Si tenemos una función 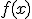 diremos que es continua en un intervalo
diremos que es continua en un intervalo 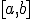 cuando sea continua en todos los puntos interiores de ese intervalo y a la derecha de a y a la izquierda de b. Gráficamente, si la función es continua en ese intervalo, vamos a poder dibujar su gráfica de un sólo trazo en ese intervalo.
cuando sea continua en todos los puntos interiores de ese intervalo y a la derecha de a y a la izquierda de b. Gráficamente, si la función es continua en ese intervalo, vamos a poder dibujar su gráfica de un sólo trazo en ese intervalo.
Pero ¿Cómo podemos saber el intervalo o intervalos en los que una función va a ser continua?, pues depende del tipo de función.
Supongamos una función 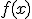 definida mediante una única expresión, por ejemplo,
definida mediante una única expresión, por ejemplo, 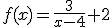
La función va a ser continua en su dominio, por lo que basta con
calcular el dominio de la función y ya tendremos los puntos en los que
va a ser continua. La razón es muy simple, en todos los puntos 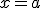 del dominio se va a cumplir que existe
del dominio se va a cumplir que existe 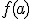 y también que
y también que 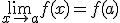 .
.
Si tenemos la función 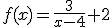
Es continua en todos los valores de los números reales menos en 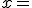 , escrito con simbología matemática, es continua en
, escrito con simbología matemática, es continua en 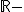 {
}
{
}
Utiliza la siguiente ventana para dibujar la función y comprobarlo:
|
|
Si tenemos la función
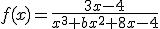
1.- Determina 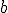 sabiendo que es discontinua en
sabiendo que es discontinua en 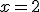 .
.
2.- Estudia otras posibles discontinuidades de la función.
3.- Comprueba tu resolución dibujando la función en la siguiente pantalla (Para saber cómo funciona puedes utilizar este manual)
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
Si la función 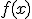 es una función definida a trozos, por ejemplo
es una función definida a trozos, por ejemplo
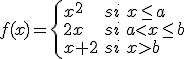
Entonces la función será continua en su dominio menos los puntos en los que se pasa de una definición a otra, en nuestro caso 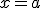 y
y 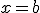 , donde habría que estudiar la continuidad.
, donde habría que estudiar la continuidad.
Ojo, puede que en estos puntos sea continua.
Practica un poco en la siguiente ventana eligiendo los valores de  y de
y de 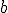 y observando cuando la función es continua, es decir, cuando su gráfica se puede dibujar de un único trazo.
y observando cuando la función es continua, es decir, cuando su gráfica se puede dibujar de un único trazo.
| Creado con GeoGebra por Manuel Sada (Abril 2005) |
Consideremos la función:
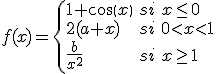
Calcula los valores de  y de
y de 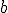 de forma que la función sea continua siempre.
de forma que la función sea continua siempre.
