1.1. ¿Qué debe pasar para no parar el coche?
Si tenemos una función 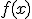 diremos que es continua en un punto
diremos que es continua en un punto 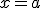 cuando se cumpla que:
cuando se cumpla que:
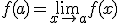
Así, se deben cumplir tres cosas:
1) Que podamos calcular 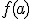 .
.
2) Que exista 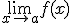 para ello sabemos que deben existir los límites laterales y coincidir, es decir:
para ello sabemos que deben existir los límites laterales y coincidir, es decir:
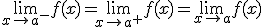
3) Por último, que la función en el punto coincida con el límite, es decir:
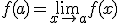
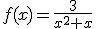 es continua en
es continua en 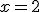
Verdadero Falso
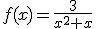 es continua en
es continua en 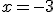
Verdadero Falso
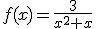 es continua en
es continua en 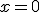
Verdadero Falso
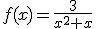 es continua en
es continua en 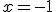
Verdadero Falso
De forma análoga a como definimos los límites laterales en el tema 2, podemos hablar de las continuidades laterales de una función.
La función f(x) es continua por la izquierda en 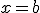 si existen
si existen 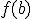 y
y 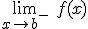 y se cumple que
y se cumple que 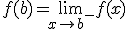 .
.
Por su parte será continua por la derecha en 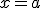 si existe
si existe 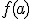 y
y 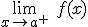 y se cumple que
y se cumple que 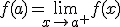 .
.
Como consecuencia de lo anterior diremos que una función 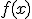 es continua en un intervalo
es continua en un intervalo 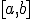 si la función es continua en todos los puntos interiores del intervalo y además es continua a la derecha de a y a la izquierda de b. Si el intervalo fuese abierto estas dos últimas condiciones sobrarían.
si la función es continua en todos los puntos interiores del intervalo y además es continua a la derecha de a y a la izquierda de b. Si el intervalo fuese abierto estas dos últimas condiciones sobrarían.
 |
| Fábrica de Esther Balgoma Hernando. Imagen obtenida del Banco de imágenes del ITE. |
Una fábrica envasadora tiene una cinta por la que circulan las botellas que van a llenarse. Las botellas se llenan a lo largo de una curva descrita por la función 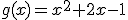 . Tras llenarse, en el punto
. Tras llenarse, en el punto 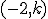 se le pone el tapón a las botellas, siguiendo por la curva anterior hasta el punto de abcisa
se le pone el tapón a las botellas, siguiendo por la curva anterior hasta el punto de abcisa 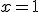 en el que las botellas deben seguir una línea recta para llegar al almacén. Todo este proceso se ha automatizado siguiendo la siguiente función:
en el que las botellas deben seguir una línea recta para llegar al almacén. Todo este proceso se ha automatizado siguiendo la siguiente función:
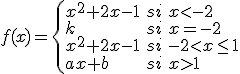
Ahora la máquina se ha desconfigurado y, puesto que la cinta que recorren las botellas no se rompe, debemos investigar sobre qué se debe cumplir para que la función sea continua en 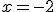 y en
y en 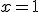 .
.
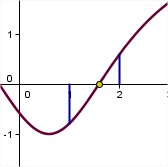
Comprueba posteriormente en el gráfico inferior que el resultado que has obtenido es el correcto.
Uno de los resultados más importantes en el tema de continuidad es el teorema de Bolzano que nos dice:
 |
Si f(x) es una función continua en el intervalo [a, b], y sí, además, en los extremos del intervalo la función f(x) toma valores de signo opuesto (es decir, se verifica f(a) · f(b) < 0), entonces existe al menos un valor 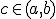 para el que se cumple: f(c) = 0. Es decir, si una función es continua en un intervalo cerrado y acotado [a, b], y los valores en los extremos del intervalo tienen signos distintos, entonces podemos asegurar la existencia de al menos una raiz de la función en el intervalo abierto (a, b).
para el que se cumple: f(c) = 0. Es decir, si una función es continua en un intervalo cerrado y acotado [a, b], y los valores en los extremos del intervalo tienen signos distintos, entonces podemos asegurar la existencia de al menos una raiz de la función en el intervalo abierto (a, b).
El teorema de Bolzano tiene una interesante aplicación en la localización de las raices o ceros de una funcion continua. Consiste en lo siguiente: buscamos por tanteo dos valores "a" y "b" para los que la función tome signos opuestos. Si conseguimos encontrar dos valores que cumplan la condición anterior, por ejemplo f(a) < 0 y f(b) > 0, y, además, la función es continua en I = [a, b], queda garantizada por el teorema de Bolzano la existencia en el intervalo (a, b) de al menos una raíz.
Si ahora tomamos el punto medio del intervalo (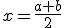 ) la función en ese punto puede tomar el valor 0, en cuyo caso ya tendríamos localizada una raíz, o bien en
) la función en ese punto puede tomar el valor 0, en cuyo caso ya tendríamos localizada una raíz, o bien en 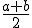 toma un valor positivo o negativo. Si f(
toma un valor positivo o negativo. Si f(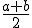 ) < 0, nos fijaríamos ahora en el intervalo I1 =[
) < 0, nos fijaríamos ahora en el intervalo I1 =[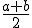 , b] en el que la función es continua y en cuyos extremos toma valores de signos opuestos. El teorema de Bolzano garantiza así la existencia de al menos una raiz en ese intervalo I1 de longitud la mitad de la longitud del intervalo inicial. Si f(
, b] en el que la función es continua y en cuyos extremos toma valores de signos opuestos. El teorema de Bolzano garantiza así la existencia de al menos una raiz en ese intervalo I1 de longitud la mitad de la longitud del intervalo inicial. Si f(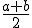 )>0 tomamos el intervalo I1=[a,
)>0 tomamos el intervalo I1=[a, 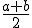 ]. Se repite el mismo proceso con el intervalo I1, con lo que vamos obteniendo intervalos cada vez más pequeños, dentro de los cuales sabemos que existe una raíz. Podemos así hallar el valor de esa raíz con la aproximación deseada.
]. Se repite el mismo proceso con el intervalo I1, con lo que vamos obteniendo intervalos cada vez más pequeños, dentro de los cuales sabemos que existe una raíz. Podemos así hallar el valor de esa raíz con la aproximación deseada.
El applet que aparece a continuación permite elegir entre dos funciones continuas y comenzar con el intervalo de partida que deseemos. Pulsando el botón "Continuar" el applet aplica el procedimiento de la bisección y muestra el siguiente intervalo dentro del cual se encuentra una raíz. Hay que tener cuidado y elegir un intervalo inicial en cuyos extremos la función tome valores de signos opuestos.
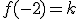
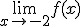 para ello vamos a calcular los límites laterales:
para ello vamos a calcular los límites laterales:
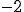
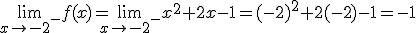
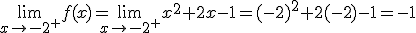
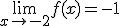
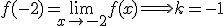
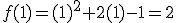
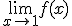 para ello vamos a calcular los límites laterales:
para ello vamos a calcular los límites laterales:
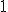
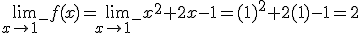
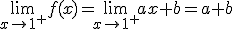
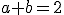
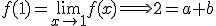 que ya se lo habíamos impuesto en el límite.
que ya se lo habíamos impuesto en el límite.
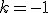 y que
y que