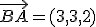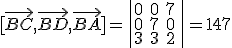2.3. Midiendo volumenes con vectores
Ya hemos analizado como podemos calcular áreas de un paralelogramo, la pregunta que nos hacemos ahora es ¿podemos calcular volúmenes ayudándonos de vectores? ¿Es posible calcular el volumen de un paralelepípedo gracias a los tres vectores que lo determinan?
Puedes observar que los paralelepípedos forman parte de nuestra vida diaria, desde una caja de zapatos, un mueble modular de un conocido fabricante Sueco de mobiliario o en construcciones arquitectónicas.
Aquí puedes apreciar algunos ejemplos de paralelepípedos.
 |
 |
|
|
Torre KIO 1 ;. Imagen obtenida desde flickr baja licencia Creative Commons
|
New Ikea TV Stand.Imagen obtenida desde flickr baja licencia Creative Commons |
En este video puedes conocer a Le Corbusier, un arquitecto frances que desarrolló su obra en la primera mitad del siglo XX y que demostró un especial amor por las matemáticas y las formas geométricas.
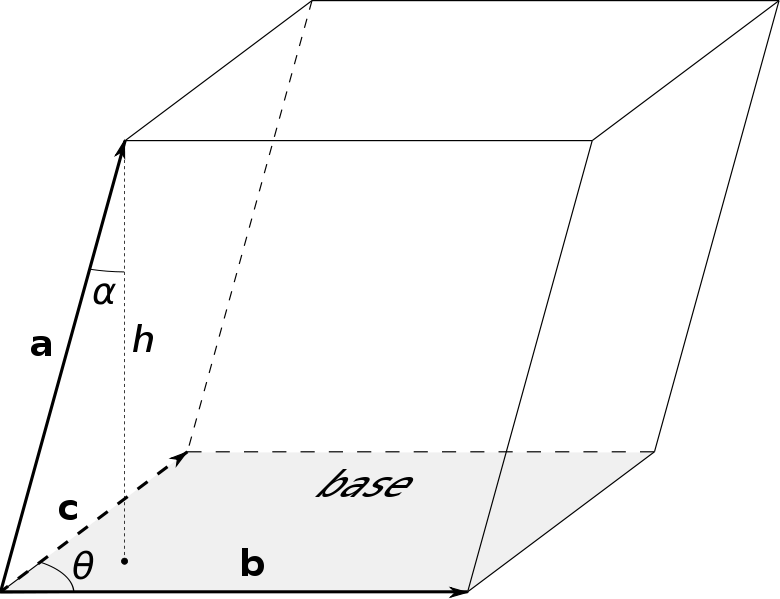 |
| Parallelepiped_volume.svg. Imagen obtenida de Wikipedia bajo licencia Creative Commons |
El área de la base formada por los vectores 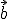 y
y 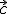 es
es 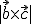 y el
y el 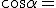
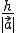 . Por lo tanto
. Por lo tanto
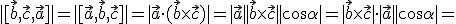
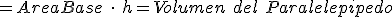
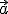 = (-1,1,2),
= (-1,1,2), 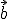 = (0,3,1) y
= (0,3,1) y 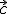 = (1,-1,3)
= (1,-1,3)
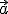 = (1,-2,2),
= (1,-2,2), 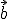 = (3,3,-1) y
= (3,3,-1) y 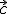 = (-3,-2,-3), calcula el volumen del paralelepípedo formado por ellos.
= (-3,-2,-3), calcula el volumen del paralelepípedo formado por ellos.
7
| |
-7
| |
0
| |
No es posible calcular el volumen
| |
En el siguiente applets, puedes apreciar como tres vectores forman un paralelogramo y calcular el volumen formado por ellos.
El applet ha sido creado por Consolación Ruiz Gil, bajo licencia Creative Commons.
El volumen del tetraedro es un sexto del volumen del paralelepípedo.
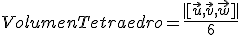
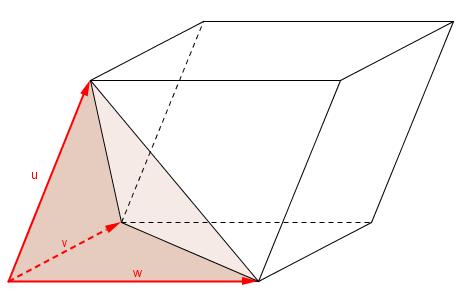
Para calcular el volumen de la "Pirámide Roja", de base triangular, se han tomado desde un satélite varias fotografias. Determina dicho volumen, teniendo en cuenta los vértices indicados en la fotografía (los vértices se han calculado mediante escala).
 |
|
La pirámide roja. Imagen obtenida de flick.com bajo licencia Creative Commons, permitiendose obras derivadas. |
Calcula el valor del tetraedro formado por los puntos A = (1,1,2), B = (-1,1,3), C = (0,1,-1) y D = (-2,-2,1).
21
| |
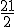
| |
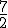
| |
Ninguna de las respuestas anteriores.
| |
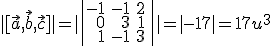
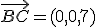 ,
, 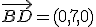 y
y