1.1. Un vector muy especial
Mueve el punto rojo y observa los nuevos vectores que obtenemos. Muévelo incluso a un nivel inferior al plano ¿Son todos perpendiculares a 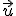 y a
y a 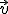 ? ¿Qué diferencias aprecias?
? ¿Qué diferencias aprecias?
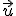 Y
Y 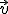 y que cumplirá una serie de características
y que cumplirá una serie de características
El producto vectorial de dos vectores linealmente independiente,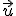 y
y 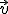 , es un nuevo vector
, es un nuevo vector 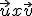 , que cumple las siguientes condiciones:
, que cumple las siguientes condiciones:
Módulo: El módulo del nuevo vector, es el producto de los módulos de 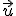 y
y 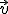 por el seno del ángulo que forman, es decir,
por el seno del ángulo que forman, es decir,
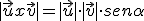
Dirección: La dirección del vector resultante del producto vectorial de 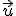 y
y 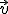 es perpendicular al plano determinado por los dos vectores.
es perpendicular al plano determinado por los dos vectores.
Sentido: Avanza en el sentido de un tornillo que rota de 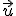 a
a 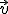
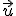 = (1,1,3) y
= (1,1,3) y 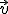 = (0,3,3)
= (0,3,3)
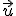 y
y 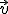 , donde
, donde 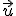 = (1,2,-3) y
= (1,2,-3) y 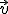 = (2,-1,1)
= (2,-1,1)
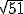
| |
7
| |
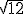
| |
-7
| |
 |
| Barraquero. Imagen obtenida del banco de imágenes del ITE |
En la definición de producto vectorial de dos vectores se ha indicado
que el sentido del vector resultante es el de un tornillo que avanza de
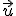 a
a 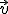 .
¿Un tornillo? ¿Qué tiene que ver un tornillo con las matemáticas? Cuando hacemos girar un tornillo en el sentido de las agujas del reloj, el tornillo avanza. Sin embargo, si lo hacemos girar en sentido antihorario, el tornillo retrocede.
.
¿Un tornillo? ¿Qué tiene que ver un tornillo con las matemáticas? Cuando hacemos girar un tornillo en el sentido de las agujas del reloj, el tornillo avanza. Sin embargo, si lo hacemos girar en sentido antihorario, el tornillo retrocede.
Debemos observar el orden del producto vectorial 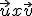 y si el giro desde
y si el giro desde 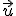 hasta
hasta 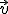 es horario o antihorario. Veamos un vídeo donde observaremos el
sentido del nuevo vector.
es horario o antihorario. Veamos un vídeo donde observaremos el
sentido del nuevo vector.
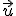 y
y 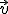 , ambos linealmente independientes, coincida con el producto vectorial de
, ambos linealmente independientes, coincida con el producto vectorial de 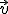 y
y 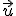
|
No, nunca.
| |
|
Sí, si los módulos de 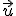 y y 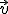 son iguales son iguales
| |
|
Si, siempre
|
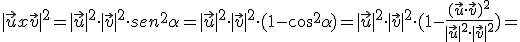
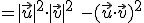
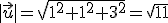 ,
, 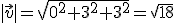 y
y 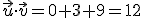 .
.