1.1. Entre dos rectas
 |
En el espacio, después de los puntos, los elementos más simples que existen son las rectas. Así que vamos a empezar por estudiar la situación en que pueden estar las rectas. A continuación tienes un ventana en la que están representadas dos rectas. Mueve los puntos P1 y P2 y los vectores 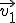 y
y 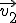 para investigar cuáles pueden ser las posiciones que tienen dos rectas en el espacio.
para investigar cuáles pueden ser las posiciones que tienen dos rectas en el espacio.
| En la siguiente escena observamos dos vectores V1 y V2 y dos puntos
P1 y P2. Hemos construido la recta que pasa por P1 y tiene por vector
director V1 y hemos construido la recta que pasa por P2 y tiene por
vector director V2.
V1 y V2 son dos vectores linealmente dependientes, es decir V1 se obtienen al multiplicar V2 por un número. Además P1 y P2 están sobre la misma recta. Observamos que las dos rectas son la misma. En la escena puedes mover de sitio el punto P1 y el P2 y observar que si no están sobre esa misma recta, las rectas que se obtienen no son la misma. Puedes cambiar los vectores V1 y V2 y observar que si son linealmente dependientes las rectas son paralelas, y si son independientes, las recats tienen distinta dirección. Instrucciones:
|
Dos rectas en el espacio pueden tener cuatro posiciones relativas:
|
 |
 |
Ejemplos de las cuatro posiciones podemos encontrarlas con facilidad en nuestro entorno cotidiano. Imaginemos que vamos circulando por una carretera si de pronto nos encontramos con otra carretera con la que hay un cruce, con los correspondientes Stop o Ceda el paso, nos encontramos con dos rectas que se cortan. Precisamente el punto de corte es el cruce. Si por el contrario la carretera cruza a distinto nivel, como pasa por ejemplo en las autovías, tenemos dos rectas que se cruzan.
Si circulamos por una autovía, nosotros marchamos por un carril y los que van en dirección contraria por otro paralelo, estaríamos en el caso de rectas paralelas. Mientras que si circulamos por una carretera comarcal, los dos sentidos circulan por la misma carretera, estaríamos en el caso de dos líneas coincidentes.
Vamos a continuación a estudiar como se halla la posición relativa de dos rectas. Consideraremos una recta r que pasa por el punto P y tiene de vector dirección 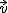 y otra s que pasando por Q tiene de dirección
y otra s que pasando por Q tiene de dirección 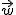 . En las siguientes presentaciones tienes dos métodos distintos de hallar la posición. Pulsa sobre ellas para avanzar.
. En las siguientes presentaciones tienes dos métodos distintos de hallar la posición. Pulsa sobre ellas para avanzar.
a) 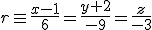 y
y 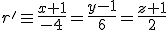
b) 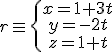 y
y 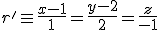
Estudia la posición relativa de las siguientes pares de rectas.
a) 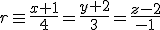 y
y 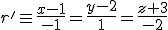
b) 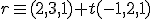 y
y 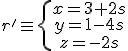
 |
Si tomamos un punto cualquiera del espacio y consideramos todas las rectas que pasan por ese punto, al conjunto de rectas que se forman se le llama Radiación de Rectas.
Si tenemos el punto 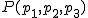 , que sería el vértice de esa radiación, la ecuación de este lugar geométrico sería:
, que sería el vértice de esa radiación, la ecuación de este lugar geométrico sería:
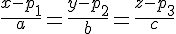
Para cada valor que le demos a la terna (a,b,c) obtendremos una recta distinta perteneciente a la radiación.
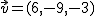 y la recta r' pasando por Q(-1,1,-1) y con dirección
y la recta r' pasando por Q(-1,1,-1) y con dirección 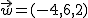 . Lo primero es ver si sus vectores dirección son proporcionales, para ello los dividimos término a término.
. Lo primero es ver si sus vectores dirección son proporcionales, para ello los dividimos término a término.
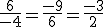 las dos rectas tienen la misma dirección. Basta ver si uno de los puntos de una de las rectas pertenece a la otra.
las dos rectas tienen la misma dirección. Basta ver si uno de los puntos de una de las rectas pertenece a la otra.
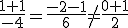 , el punto no pertenece a la recta y por tanto las rectas son paralelas.
, el punto no pertenece a la recta y por tanto las rectas son paralelas.
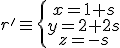 e igualamos las variables
e igualamos las variables 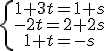
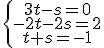 y estudiamos los rangos de
y estudiamos los rangos de 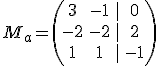 .
.
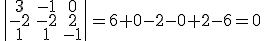 Luego rango(Ma)=2.
Luego rango(Ma)=2.
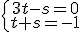 sumamos las ecuaciones y obtenemos
sumamos las ecuaciones y obtenemos 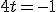 , luego
, luego 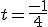 , basta sustituir ese valor en la recta r y obtenemos el punto de corte:
, basta sustituir ese valor en la recta r y obtenemos el punto de corte: 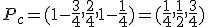 .
.