2. Especial Selectividad
Sean la recta 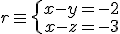 y la recta
y la recta 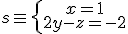 .
.
a) Estudia la posición relativa de r y s.
b) Halla la ecuación del plano que contiene a s y es paralelo a r.
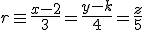 y
y 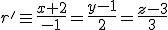
a) Halla k sabiendo que las rectas r y s se cortan en un punto.
b) Determina la ecuación del plano que contiene a las rectas r y s.
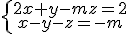 y el plano definido por
y el plano definido por 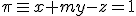
a) ¿Existe algún valor de m para el que la recta y el plano sean paralelos?
b) ¿Para qué valor de m está la recta contenida en el plano?
c) ¿Cuál es la posición relativa de la recta y el plano cuando m=0?
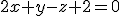 y la recta
y la recta 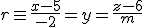 .
.
a) Halla la posición relativa de la recta y el plano según los valores del parámetro m.
b) Para m=-3 halla el plano que contiene a la recta r y es perpendicular al plano.
c) Para m=-3, halla el plano que contiene a la recta r y es paralelo al plano.
Se sabe que los planos siguientes se cortan en una recta.:
x+2y+bz=1, 2x+y+bz=0, 3x+3y-2z=1.
a) Calcula el valor de b.
b) Halla unas ecuaciones paramétricas de la recta.
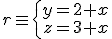 , por tanto,
, por tanto, 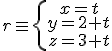 .
.
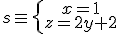 y nos queda
y nos queda 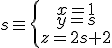 .
.
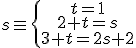 , de las dos primeras ecuaciones obtenemos los valores t=1 y s=3 que al sustituir en la tercera ecuación comprobamos que no la cumple, ya que,
, de las dos primeras ecuaciones obtenemos los valores t=1 y s=3 que al sustituir en la tercera ecuación comprobamos que no la cumple, ya que, 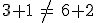 . Luego el sistema no tiene solución, y como los vectores de dirección no son proporcionales, las dos rectas se cruzan en el espacio.
. Luego el sistema no tiene solución, y como los vectores de dirección no son proporcionales, las dos rectas se cruzan en el espacio.
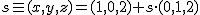 y
y 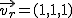 .
.
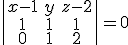 y al desarrollar obtenemos la ecuación del plano pedido:
y al desarrollar obtenemos la ecuación del plano pedido: 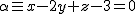 .
.
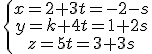 reordenamos el sistema
reordenamos el sistema 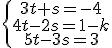 .
.
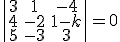 desarrollamos y queda
desarrollamos y queda 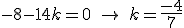 que es el valor de k pedido.
que es el valor de k pedido.
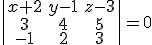 y queda el plano:
y queda el plano: 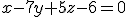
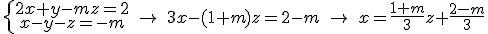 sustituimos en la segunda ecuación y despejamos la y
sustituimos en la segunda ecuación y despejamos la y 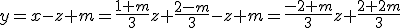 por lo tanto tenemos
por lo tanto tenemos 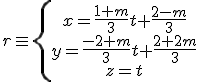 . Sustituimos en el plano y operamos.
. Sustituimos en el plano y operamos.
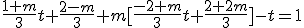 Multiplicamos todo por 3, para quitar denominadores y quitamos paréntesis
Multiplicamos todo por 3, para quitar denominadores y quitamos paréntesis 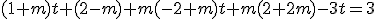 y entonces nos queda
y entonces nos queda
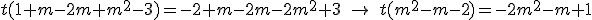
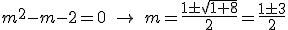 Hay por tanto dos valores m=2 y m=-1 que hacen cero el paréntesis. Veamos entonces los casos que nos piden.
Hay por tanto dos valores m=2 y m=-1 que hacen cero el paréntesis. Veamos entonces los casos que nos piden.
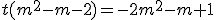 tiene solución única y por tanto la recta y el plano se cortan. Por ejemplo para m=0 la ecuación queda -2t=1 despejando la t obtenemos:
tiene solución única y por tanto la recta y el plano se cortan. Por ejemplo para m=0 la ecuación queda -2t=1 despejando la t obtenemos: 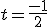 y en este caso la recta y el plano se cortan en el punto de coordenadas:
y en este caso la recta y el plano se cortan en el punto de coordenadas: 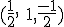
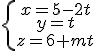 en el plano
en el plano 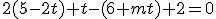 y operamos
y operamos
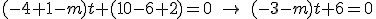
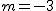 se anula el paréntesis y el sistema no tiene solución por lo que la recta es paralela al plano.
se anula el paréntesis y el sistema no tiene solución por lo que la recta es paralela al plano.
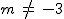 podemos despejar t y hay una única solución. La recta corta al plano.
podemos despejar t y hay una única solución. La recta corta al plano.
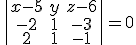 y nos queda
y nos queda 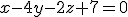 .
.
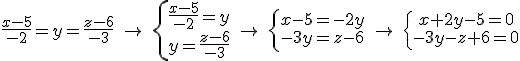
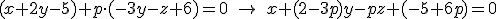
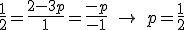 por lo que el plano es
por lo que el plano es 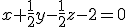 o bien
o bien 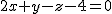 .
.
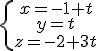 .
.