3.2 Algunos ejemplos de interés.

|
|
12. Imagen de hispaniainfo en wordpress.com bajo licencia de Creative Commons |
Un ejemplo claro de interpolación lineal lo tenemos en la declaración anual del IRPF. Cada año hacemos la declaración de la renta con una escala de gravamen cuyas cantidades se revisan anualmente.
En la tabla siguiente puedes ver la base imponible, cuota íntegra y el porcentaje aplicable:
| desde | cuota íntegra | % a aplicar al resto |
| 0 | 0 | 15 |
| 4000 | 600 | 24 |
| 13800 | 2952 | 28 |
Para una renta, por ejemplo de 6000 € a su cuota íntegra mínima 600 se le sumará la diferencia a 4000, es decir, 2000, por 24 %; 600+(6000-4000)x0,24=600+480=1.080 €.
Cojamos los puntos (0, 0) (4000, 600) para hallar la recta de interpolación:
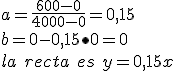
la pendiente "a" de la recta es el % que corresponde a ese tramo y el cálculo de la base imponible que se encuentre entre 0 y 4000 se calcula con la recta calculada, siendo "x" la renta e "y" la base.
Para los puntos (tramos) (4000, 600) y (13800, 2952)
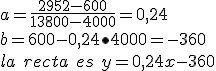
Si tenemos una renta de 6000 € nuestra base imponible sería de y=0,24·6000-360=1080 €

|
| 13. Imagen fluzo bajo licencia de Creative Commons |
Como recordarás del punto 1 del tema, Evaristo tiene anotado en una tabla la relación entre sus ingresos y ahorros. ¿Cuál es la recta que le permite interpolar y extrapolar el ahorro en función de los ingresos? ¿Según los datos de que disponemos se cometen errores? ¿Qué cantidad ahorrará para el próximo año si tiene previsto ganar 65.000 €?
| Ingresos (en miles) | 54 |
56 |
58 |
62 |
| Ahorro (en cientos) |
20 |
22 |
24 |
28 |
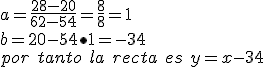
Donde la "x" son los ingresos en miles y la "y" el ahorro en cientos. Como habrás observado la recta la hemos obtenido con los datos del primer y el último año. ¿Coincidirá el ahorro de los años intermedios?
En la tabla la fila de los ingresos (x) le restas 34 y coinciden con los datos reales. Todos los puntos están alineados y pertenecen a la recta y=x-34.
Puesto que el error no existe en la estimación, para este año 65-34=31 habrá ahorrado 3.100 euros.
|
0,28
| |
|
28 %
| |
|
3,57
|
|
y=0,28x+912
| |
|
y=0,28x-912
| |
|
y=912x-0,28
|
|
3000 €
| |
|
No se puede calcular por estar fuera del tramo.
| |
|
4688 €
|
 |
- Por cada kilómetro más que viaje tiene que pagar €.
- La bajada de bandera cuestoa €.
- Si realiza en las mismas condiciones un viaje de 10 kilómetros deberá pagar €.
- Mientras que si el viaje fuese de 2o kilómetros el valor de la carrera ascendería a €
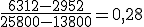
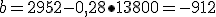 , la recta es y=0,28x-912
, la recta es y=0,28x-912
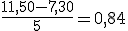 .
.
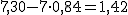 .
.
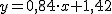 .
.
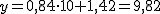 y por 20 será
y por 20 será 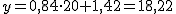 .
.