3.1 Extrapolación
Actividad
Cuando se realiza una estimación para valores que se encuentran fuera del rango (mayores que el máximo o menores que el mínimo) de los datos que poseemos, el proceso se denomina extrapolación.
Este procedimiento conlleva un mayor riesgo de error, al suponer que el comportamiento de la función fuera del intervalo es el mismo que dentro de él.
|
|
10. Tormenta Imagen de qlio bajo licencia de Creative Commons |
Hay condiciones que la extrapolación no puede predecir. Te pongo ejemplos:
Un agricultor que en cinco años recoge un 5% más cada año puede predecir, que con esos datos el próximo año puede conseguir aumentar su cosecha en un cinco por ciento, pero nada puede predecir las tormentas, falta de agua, etc.
No todo puede ser culpa de fenómenos naturales, puede ser, como es el caso del consumo de un automóvil visto en el apartado 2.1, que no siga una función lineal y por tanto la predicción sea errónea.
Ejemplo o ejercicio resuelto
 |
|
11.Educación:Imagen en mundosparalelos.me bajo licencia de Creative Commons |
Recuerda la tabla que te proponíamos en la introducción del apartado 3
| Año | 1994 | 1995 | 1996 |
| Gasto en educación (miles de millones ptas.) | 4002,5 | 4300,2 | 4569,5 |
¿qué gasto se espera en educación en los años 1997 y 1998?
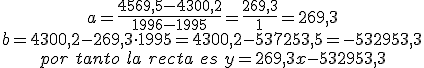
Calculemos el gasto previsto para 1997.
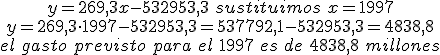
Para el año 1998 operamos igual, es decir,
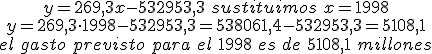
Ahora, bien si consultamos los gastos reales para esos años en educación veremos que en el 1997 fue de 4780,5 y en 1998, 5036,7.
AV - Pregunta de Selección Múltiple
| Ingresos en miles |
58 | 62 |
| Gasto en ropa en miles |
2 | 5 |
1.- ¿La recta que interpola el gasto de ropa en función de los ingresos es?
y-2=0,75(x-58)
| |
y=0,75x-41,5
| |
y=0,75-41,5x
| |
7.250 €
| |
7,25 €
| |
7,25 en cientos de euros
| |
48708,5 €
| |