2.2. Se cometen errores
Ejemplo o ejercicio resuelto
|
|
8. Badajoz:dip-badajoz.es bajo licencia de Creative Commons |
En la siguiente tabla aparecen los habitantes de la provincia de Badajoz:
| Año | 2005 | 2007 |
| N.º de habitantes |
671.299 | 678.459 |
¿Qué población se calcula que tenía en el 2006?
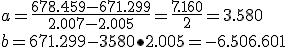
por lo tanto la recta es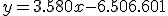 
.
Calculando para x=2006 nos quedarían
 |
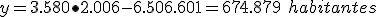
Es decir, segun nuestros cálculos, Badajoz debía de tener 674.879 habitantes. Ahora bien si consultamos la base de datos del INE ese año la población de Badajoz fue de 673.474.
A esta diferencia (-1.405) la llamamos error absoluto de interpolación.
Error de interpolación
A la diferencia entre el valor real (y*) y el estimado (y) se le llama error de interpolación.
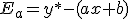
En nuestro ejemplo anterior y*=673.474 e y=674.879, entonces Ea=-1405. La provincia de Badajoz, en el año 2006, tenía 1405 habitantes menos que el valor que hemos hallado en nuestra estimación por interpolación lineal.
Para saber más
Con el fin de minimizar el error de interpolación, cuando tres puntos no están alineados también podemos interpolar con una función del tipo y=ax2+bx+c.
A esta interpolación se le llama cuadrática
 |
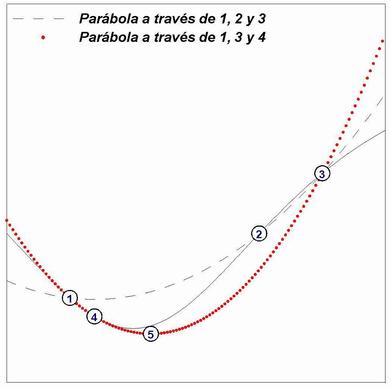Para tres puntos no alineados (x1,y1) (x2,y2) y (x3,y3)
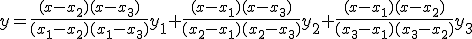
Veamos el ejemplo: (0,2), (1,2) y (2,4)
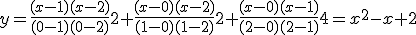
En la escena que viene a continuación puedes determinar la ecuación de la parábola que define tres puntos. Puedes moverlos por la escena y ver la ecuación de dicha función cuadrática:
Applet modificado del original de José Luis Abreu León en Descartes bajo licencia Creative Commons.
AV - Pregunta Verdadero-FalsoMarca si es falso o verdad en las cuestiones que se plantean.
1.- En la interpolación lineal es necesario conocer al menos 3 puntos.
Verdadero Falso
2.- Tres puntos siempre están alineados
Verdadero Falso
3.- Por los puntos (1,3) (2,6) y (4, 12) pasa una única recta.
Verdadero Falso
4.- El error que cometemos al considerar el punto (3,11) como punto de la recta anterior (y=3x), es de 2 unidades.
Verdadero Falso