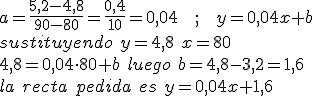2.1. Se puede hacer a ojo y conocer la fómula

7. A ojo:Imagen de verdaderonoga bajo licencia de Creative Commons

Cualquiera de los ejemplos de los apartados anteriores se podían haber resuelto utilizando un sencillo cálculo:

85 es el punto medio de 80 y 90 con consumos 4,8 y 5,2, calculando la media de estos consumos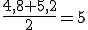

Vas por la autovía circulando a una velocidad media de 120 km/h y ves el cartel a Zaragoza 90 km. ¿qué tiempo nos falta para el trayecto?

Basta con dividir por 2, es decir, 45 minutos. Esta estimación tiene su fundamentación matemática. Cuando circulamos a 60 km/h, recorremos 1 km por minuto, por tanto, a 120 km/h la distancia en kilómetros es el doble que el tiempo en minutos.

Sabiendo estas relaciones, y utilizando el método del punto medio, a 90 km/h ¿cuál es la proporción km y minutos?

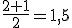
Ahora verás que las matemáticas te ofrece solución para conocer la función con la que puedes interpolar.

Interpolación Lineal

Conocidos dos puntos A(x₁, x₂); B(y₁, y₂) la función lineal que definen es y=ax+b donde:

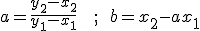
Al coeficiente "a" se le llama pendiente y al "b" ordenada en el origen, como ya viste al trabajar la función lineal en el tema 3 de la anterior Unidad.

Por ejemplo la función lineal que contiene a los puntos A(2,5) y B(4,-1) sería y=-3x+11 ya que

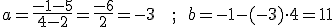
En la siguiente escena, también podemos determinar la recta que une dos puntos. Puedes mover libremente los puntos y en cada momento se está calculando la recta que los une.

Para coger práctica, puedes colocar los puntos en varias posiciones, hacer tú la recta y comprobar después que te sale bien.

Applet modificado del original de José Luis Abreu León en Descartes bajo licencia Ceative Commons.

Ejemplo o ejercicio resuelto

En un folleto informativo de cierta inmobiliaria presentan la siguiente información:

Venta de pisos desde 60.000 € hasta 120.000 €. El edificio tiene 16 plantas y los precios se encarecen, así lo marca el folleto, con la altura.

¿Cuál es la función lineal definida para los pisos de la 1ª y 16?

Apliquemos las fórmulas dadas a los puntos A(1,60) y b(16,120):

Calculemos "a"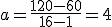

la función es y=4x+b y tiene que pasar por el punto (1,60) sustituyendo, tenemos 60=4·1+b; despejando "b", b=56.

La función lineal que interpola los puntos A y B es y=4x+56. Donde x toma valores de 1 a 16 (nº de planta) e y es el precio en miles de euros.

Observa que para cada valor de x obtendríamos los valores de y que nos proporcionaron en la tabla del apartado 1 de este tema.

Planta (x)	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Precio (y)	60	64	68	72	76	80	84	88	92	96	100	104	108	112	116	120

Observa el gráfico:

Todos los puntos están alineados, es decir, pertenecen a la misma recta. ¿pero que pasaría si ello no ocurriera?

Actividad

Dados tres puntos A(x₁ ,x₂); B (y₁,y₂) y C(z₁,z₂) se dice que están alineados si C pertenece a la recta que pasa por los puntos A y B.

Si y=ax+b es la recta que interpola a A y B , entonces C está alineado con A y B si:

z₂=az₁+b

Por ejemplo, si tenemos los puntos A(-1,2), B(2,9) y C(5,15) para ver si están alineados hallamos la recta que pasa por A y B, que sería y=2x+5, y comprobamos si C pertenece a ella o no, es decir, vemos si verifica la ecuación. En este caso si pertenece ya que 2·5+5 = 15.

Ejemplo o ejercicio resuelto

¿Recuerdas la tabla que relacionaba la velocidad de un automóvil con el consumo?

A la izquierda tienes el gráfico en un sistema de ejes. La línea roja que une los puntos dos a dos muestra que al menos tres de ellos no están alineados, ¿podríamos demostrarlo analíticamente?

Por otra parte, la recta que definen los dos últimos puntos (color negro) no pasa por los dos primeros ¿lo probamos también?. Y finalmente ¿qué consecuencia podemos sacar de la relación de estas dos variables?

Precio Súper A	10	12	20
Precio Súper B	8	10	18