2. Cuando la relación se convierte en función.
En la vida cotidiana hay muchos asuntos que están relacionados entre sí. Seguramente tu sueldo depende del número de horas que trabajes a la semana, tu salud dependerá de lo que cuides tu dieta y el ejercicio físico que estés acostumbrado a realizar, el número de horas que descanses cada día influye en tu rendimiento diario. En muchas de esas relaciones, un valor de uno de los elementos sólo puede estar relacionado con un valor del otro.
 |
| 4. Imagen tomada de ISFTIC bajo licencia Creative Commons. |
Por ejemplo, el aumento o disminución del IPC durante el pasado mes de diciembre no puede tener varios valores, sino sólo uno. Si viajas de tu ciudad hasta otra lejana, el tiempo que tardes es único, puede variar según el medio de transporte y las situaciones que se den, pero está claro que no puedes tardar en el mismo viaje siete horas y cuarto y a la vez tres horas y media.
Estas situaciones son muy corrientes en las relaciones entre elementos y van a dar lugar a un nuevo objeto matemático: las funciones.
Importante
Llamaremos función a toda relación entre dos conjuntos de números de forma que a cada elemento del primer conjunto le corresponde un único elemento del segundo.
Por ejemplo, el número de nacimientos en España durante los años del pasado siglo XX o la relación entre la medida del lado de un salón cuadrado y la superficie del suelo donde se quiere colocar una moqueta.
Importante
En toda función se relacionan dos tipos de elementos numéricos. El primero se llama variable independiente, pues toma cualquier valor sin depender de nadie. Suele representarse por la letra x. El segundo recibe el nombre de variable dependiente pues su valor depende del valor de x. Suele representarse por la letra y.
Por ejemplo, las ganancias que tenga un concesionario de automóviles dependen del número de coches que venda. El número de coches es la variable independiente y las ganancias sería la variable dependiente.
Cuando un valor y depende del valor de x suele decirse que "y es función de x" y se representa en la forma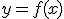 
.
El valor que toma la variable independiente suele llamarse antecedente y el que toma la variable y, imagen.
Curiosidad
La palabra función proviene del latín functio que significa ejecución.
También deriva del latín la palabra variable, en este caso de variare que significa modificar o transformar.
Del griego graphikós, que significa dibujar, proviene la palabra gráfica, que usaremos más adelante.
AV - Actividad de Espacios en Blanco
En las siguientes situaciones correspondientes a una función indica cuál es la variable independiente y cuál la variable dependiente.
Escribe en el espacio en blanco las palabras independiente o dependiente.
a) En una determinada calle, consideramos la función que relaciona el número de personas que viven en una casa con el número de la casa.
El número de personas es la variable .
El número del portal de la casa es la variable .
b) En una refinería de petróleo se relaciona el número de camiones que reparten la gasolina por las ciudades y la cantidad de gasolina que se reparte.
El número de camiones es la variable .
La cantidad de petróleo repartido es la variable .
c) En las fiestas de Navidad se relaciona el número de empleados de Correos que tienen que repartir la avalancha de correo extraordinario con el tiempo que tardan en hacerlo.
El número de carteros será la variable .
El tiempo que se tarde en hacer el reparto es la variable .
 |
Ya hemos dicho que en toda función se relacionan dos conjuntos de números. Esos conjuntos de números pueden ser más o menos grandes, según la situación en la que nos encontremos. Para hacer referencias a ellos utilizaremos unos nombres especiales.
Importante
Se llama dominio de definición de la función, o simplemente dominio, al conjunto de valores que puede tomar la variable independiente, se suele representar por D o Dom(f). Llamamos recorrido al conjunto de valores que toma la variable dependiente y se representa por R o Im(f).
Si consideramos la recaudación de una sala pequeña de un multicine con cabida para 50 personas, el dominio estaría formado por todos los valores comprendidos desde cero, cuando está la sala vacía, hasta 50, cuando la sala está llena. El recorrido serían los valores desde cero hasta el valor máximo de la recaudación, que sería, si suponemos la entrada a 7 euros, un total de 350 €.
AV - Actividad de Espacios en Blanco
Considera las siguientes funciones y los siguientes dominios de definición:
| FUNCIONES: |
| a) La mortalidad infantil anual durante la primera mitad del siglo XX. |
| b) La temperatura en una ciudad a lo largo de un dia. |
| c) Tiempo utilizado por un corredor en una carrera de maratón. |
| DOMINIOS DE DEFINICIÓN: |
| 1) Los valores entre 0 y 24. |
| 2) Los números entre 0 y 42. |
| 3) Los números entre 1901 y 1950. |
Relaciona cada función con su dominio de definición. Escribe unicamente el número sin el paréntesis.
| a | - | |
| b |
- |
|
| c | - |
Para saber más
En la lámina, a la que accedes desde el siguiente enlace, puedes encontrar algunas características de una función.