3. Formas de expresar una relación funcional.
Seguro que después de ver el apartado anterior estás descubriendo que muchas relaciones que se dan en tu vida diaria son realmente funciones, con lo que te resultará satisfactorio saber que manejas funciones desde hace tiempo, aún sin saberlo.
 |
La ventaja de las funciones es que hay varias formas de expresarlas, por lo que relaciones funcionales muy diversas pueden aparecer ante ti de una manera u otra. Desde el gasto en comida a lo largo de un mes, la estatura o peso que vas teniendo a lo largo de una temporada o el crecimiento de una planta durante su vida.
Las distintas formas de expresar una función son las siguientes:
1) Mediante una frase o enunciado.
Si pensamos en Patricia, que la tenemos un poco abandonada, la relación entre su sueldo del mes y el trabajo realizado en la notaría es sin duda una función. Según nos comentaba ella misma, cobra 500 euros mensuales fijos por el trabajo rutinario que realiza. Además, le encargan preparar la documentación para algunos de los casos que tiene que supervisar el notario, y por ello cobra 100 euros extra por cada documentación completa.
Podemos ver que con esa frase tenemos perfectamente determinada la función.
2) Mediante una tabla de valores.
Ya comentamos en apartados anteriores que una función era una relación entre pares de números, por ello, si escribimos una tabla donde se relacionen los valores de la variable independiente con los de la dependiente, también tendremos definida la relación funcional.
En el caso de Patricia, la variable independiente sería el número de casos que prepara y la dependiente el dinero que cobra a fin de mes. Y una gráfica de valores podría ser:
| nº de casos preparados |
0 | 1 |
2 |
3 |
4 |
| sueldo a fin de mes |
500 | 600 |
700 |
800 |
900 |
3) Mediante una gráfica.
En los medios de comunicación cada vez es más corriente la presentación de datos mediante una gráfica, pues de un vistazo se puede apreciar la evolución de la relación funcional sin necesidad de atender a valores individuales.
|
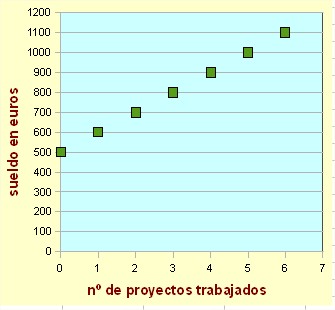
Recuerda que una gráfica se obtiene al representar en unos ejes de coordenadas, una serie de puntos cuyas coordenadas representan valores relacionados mediante una función, por ejemplo, en la tabla anterior tienes pares de puntos cuya primera coordenada es el número de proyectos y la segunda es el sueldo que se percibe después de haber realizado esos proyectos.
Para el caso de Patricia la gráfica que quedaría sería la siguiente:
La primera persona que se considera en la historia que utilizó las gráficas fue el obispo francés Nicolás de Oresme (1320 - 1382), quien alrededor de 1360 comienza a expresar mediante líneas la evolución de algunos fenómenos físicos como movimientos celestes. Si quieres conocer unos sucintos datos biográficos sobre este personaje haz clic en el siguiente enlace.
Ya en la unidad anterior trabajaste con las expresiones algebraicas y viste cómo expresar relaciones mediante símbolos. En el caso de las funciones puedes aplicar esos conocimientos que adquiriste.
En general se representa por x la variable independiente y por y la dependiente y se suele escribir la función de la forma y= a una expresión en la que aparece la x.
En el caso de Patricia si representamos por "x" el número de
proyectos realizados y por "y" el sueldo recibido, la expresión sería 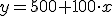 .
.
 |
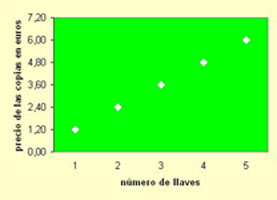
En el portal del bloque de pisos donde se ubica la notaría en que trabaja Patricia, han cambiado la cerradura que se había estropeado. Ahora deben sacar copias para los que trabajan allí y Patricia se ha ofrecido a hacerlo ella, porque tiene una ferretería al lado de su casa.
Al preguntar, le han dicho que el precio de copia de la llave que les muestra es de 1.20 euros la unidad.
Dada que esa frase nos presenta una función que relaciona el número de llaves que tiene que hacer (que podemos representarlo por x), y el precio que le va a costar hacer las x copias (que utilizaremos el valor y para representarlo), halla cuál sería la expresión algebraica de esa función, haz una tabla de valores de lo que costarían hasta cinco llaves y representa la función.
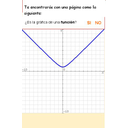
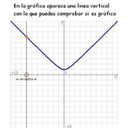
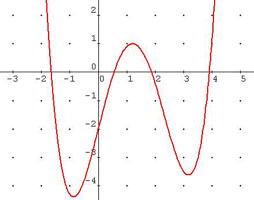
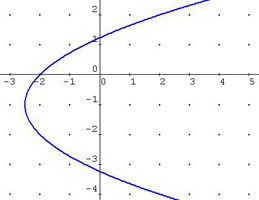
Acabamos de ver que una función puede definirse o expresarse mediante una gráfica, pero hay que tener cuidado, porque no todas las gráficas representan una función. Hay que recordar que la condición para ser función es que a todo número del dominio le corresponda un único valor. Si en una gráfica vemos que hay varios valores que corresponden a un mismo valor, entonces no representa una función. Basta levantar una recta vertical, si en algún momento corta a la gráfica en más de un punto, entonces no es función. Puedes ver la diferencia en las imágenes.
 |
 |
| Esto es función |
Esto no es función |
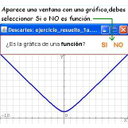
El ISFTIC tiene un proyecto de Educación digital a distancia donde puedes encontrar las matemáticas de 4º de ESO, en la opción B, totalmente desarrollada de forma interactiva. Dentro de ese conjunto de actividades hay una con la que puedes practicar para saber si una gráfica es o no función. Puedes acceder a esa actividad desde el siguiente enlace, pero antes de hacerlo haz un recorrido por la galería de imágenes para que sepas los pasos debes dar.
 |
| 5. Foto de Pablo Mª García Llamas tomada de ISFTIC bajo licencia Creative Commons. |
Los problemas van a aparecer con las funciones que no pueden expresarse mediante una expresión algebraica. Por ejemplo, la función que da el peso de un recién nacido durante su primer año de vida es muy difícil, por no decir casi imposible, presentarla mediante una expresión algebraica, mientras que utilizando una tabla o una gráfica es fácil de hacer.
Como ves, hay mucha variedad para expresar una función. El problema que se nos plantea ahora es el siguiente: ¿cómo pasamos de una forma a la otra?
En general, si tenemos la expresión algebraica o el enunciado que caracteriza a la relación, es muy fácil construir una tabla, pues basta darle valores a una variable y encontrar los valores relacionados con ellos. Una vez que tenemos la tabla de valores, se obtiene con facilidad la gráfica.
A partir de la gráfica podemos construir una tabla de valores y, a veces, la expresión algebraica de la función, siempre que sea una relación fácil de deducir.
Para trabajar estas relaciones, realiza las siguientes actividades (2 actividades o 2 pantallas) de Jclic tomadas, como la anterior, del trabajo de Valle Mayoral Rivera.
|
Para practicar
Para sacar información de una gráfica basta fijarse en los valores que están representados. Si quieres practicar este concepto entra en la actividad a la que te lleva el siguiente enlace. Para trabajar con lo que hemos visto aquí, debes modificar en la parte izquierda dos datos, en primer lugar, el nivel debes situarlo en 1, para que aparezca una sola gráfica. Además, selecciona la opción de líneas para que no aparezcan diagramas estadísticos de barras.
|
| |
¿Eres uno de tantos que tiene su vivienda hipotecada? ¿Tu economía doméstica depende del interés que tienes que pagar cada mes al banco por la dichosa hipoteca? Entonces, está actividad te va a interesar mucho. En el gráfico de la derecha se muestra la evolución del Euribor a lo largo del año 2008.
Normalmente, el Euribor se expresa con dos decimales, pero para facilitar la interpretación de esta actividad, se ha redondeado a la primera cifra decimal.
Completa la tabla inferior a la vista de cómo ha cambiado este popular índice de referencia de los créditos hipotecarios.
| Mes | Euribor |
| 2 |
|
|
|
5,4 |
|
|
5,2 |
| 12 |
|
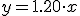 .
.