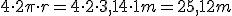1.4 Desplazamiento y espacio recorrido
Cuando un objeto cambia su posición, su vector de posición también se modifica. El vector desplazamiento es precisamente la diferencia entre los vectores de posición final e inicial
(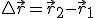 ).
).
Si te fijas en la siguiente animación, la diferencia de dos vectores es otro vector que comienza en el extremo del vector inicial y termina en el extremo del vector final. Observa que si cambias los vectores inicial o final (tanto su módulo como su dirección o sentido), también cambiará el vector desplazamiento. Para ello sólo tienes que arrastrar los extremos de los mismos.
|
|
| Simulación de Jesús Peñas bajo licencia Creative Commons |
El módulo del vector desplazamiento se conoce como desplazamiento, y es una magnitud escalar.
El espacio recorrido es la longitud de la trayectoria descrita por el móvil. Solamente coincide con el módulo del vector desplazamiento si la trayectoria es rectilínea y no hay cambio de sentido en el movimiento. Fíjate en la siguiente animación y verás que el módulo del vector desplazamiento (longitud de la flecha roja) no tiene el mismo valor que la longitud de la trayectoria (línea azul); sólo coincidirían si la trayectoria fuese recta.
|
|
| Simulación de Jesús Peñas bajo licencia Creative Commons |
Un tren de juguete recorre una pista circular de 1 m de radio. Partiendo de la caseta de la estación, da cuatro vueltas, quedándose en reposo otra vez en el punto de partida.
|
El vector desplazamiento es nulo y el espacio recorrido es cero
| |
|
El vector desplazamiento es nulo y el espacio recorrido es de unos 25 metros
| |
|
El módulo del vector desplazamiento es mayor que cero y el espacio recorrido también |
Marca la respuesta o respuestas correctas.
|
Es lo mismo trayectoria que desplazamiento
| |
|
El desplazamiento es un vector y la longitud de la trayectoria es un escalar
| |
|
La descripción del movimiento es independiente del sistema de referencia
| |
|
Nunca coinciden desplazamiento y espacio recorrido
|

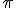 r metros
r metros