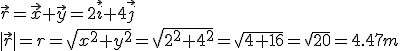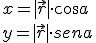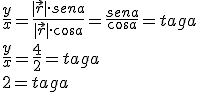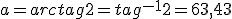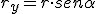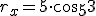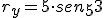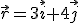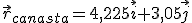1.3 Expresión de la posición
- Rectilíneo: La trayectoria es una línea recta.
- Curvilíneo:
- Circular: La trayectoria es una circunferencia.
- Elíptico: La trayectoria es una elipse.
- Parabólico: La trayectoria es una parábola.
- Irregular.
| Imagen de elaboración propia. |
Recuerda que, cuando antes hemos hablado del movimiento, hemos visto que éste es relativo, pues depende del sistema de referencia que escojamos. Y, como puedes ver en la siguiente animación, la forma de la trayectoria también depende del observador
|
|
| Animación de Jesús Peñas bajo licencia Creative Commons |
Posición
El punto en el que se encuentra un móvil en un instante determinado puede venir dado por:
- Las coordenadas del punto.
Debes tener en cuenta que si trabajamos en una dimensión, en realidad sólo habrá una coordenada para el punto (x). En un sistma bidimensional, las coordenadas de cualquier punto vendrán dadas por el par (x, y). En cambio, en un espacio tridimensional, las coordenadas de un punto presentan tres componentes (x, y, z).
A partir de ahora trabajaremos en dos dimensiones.
- El vector de posición (
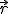 ), que es un vector que tiene su origen en el origen de coordenadas del sistema de referencia y su extremo en el punto en cuestión.
), que es un vector que tiene su origen en el origen de coordenadas del sistema de referencia y su extremo en el punto en cuestión.
Componentes cartesianas del vector de posición
Recuerda que cuando escribimos 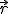 , la flecha indica que la magnitud es vectorial, mientras que si no hay flecha se indica el módulo del vector,
, la flecha indica que la magnitud es vectorial, mientras que si no hay flecha se indica el módulo del vector, 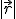 o
o  . En el vector de posición, el módulo representa la distancia al origen.
. En el vector de posición, el módulo representa la distancia al origen.
En lugar del propio vector, con mucha frecuencia se trabaja con sus componentes. Las componentes cartesianas de un vector son los vectores que se obtienen al proyectarlo sobre los ejes de un sistema de coordenadas situado en el origen del vector.
¿Cómo se obtienen las componentes de un vector? En este caso, es muy sencillo, ya que las dos componentes están en la dirección de los ejes horizontal y vertical, x e y. Es decir, el vector de posición es la suma de su vectores componentes. También se suelen escribir las componentes en función de los vectores unitarios en los dos ejes.
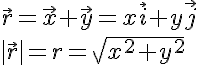
Componentes polares del vector de posición
El vector de posición 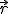 no sólo puede venir definido por sus componentes cartesianas, sino por otras componentes llamadas componentes polares. En este caso, sólo es necesario conocer el módulo del vector y su dirección, expresada como el ángulo que forma el mismo respecto al eje X.
no sólo puede venir definido por sus componentes cartesianas, sino por otras componentes llamadas componentes polares. En este caso, sólo es necesario conocer el módulo del vector y su dirección, expresada como el ángulo que forma el mismo respecto al eje X.
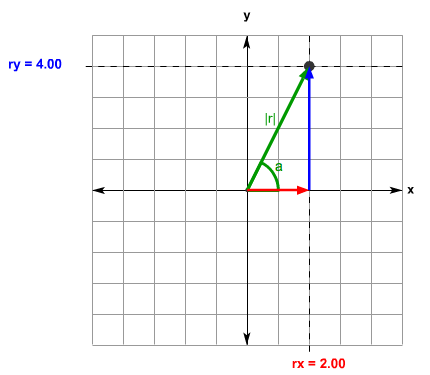
No obstante, se pueden relacionar las componentes cartesianas con las componentes polares de cualquier vector. Veamos el caso para el vector de posición.
Supongamos que
conocemos el módulo 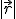 del vector
del vector 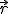 y el ángulo
y el ángulo  , que forma el vector con el eje x. Mediante el coseno y el seno del ángulo podemos obtener las componentes del vector en el eje x (
, que forma el vector con el eje x. Mediante el coseno y el seno del ángulo podemos obtener las componentes del vector en el eje x (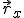 ) y en el eje y (
) y en el eje y (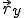 ).
).
Con la siguiente animación podrás practicar en el cálculo de componentes cartesianas a partir de componentes polares. Fíjate que puedes desplazar el punto, por lo que puedes cambiar el módulo y el ángulo respecto al eje x del vector.
Date cuenta que en el fondo ambos tipos de coordenadas permiten localizar a un objeto en el plano. En el caso de las coordenadas cartesianas dando la distancia a cada uno de los ejes y en el caso de las polares, indicando la distancia al origen de coordenadas y el ángulo que forma el vector de posición con el eje x.
|
|
| Simulación de Jesús Peñas bajo licencia Creative Commons |
Autoevaluación
Utilizando el simulador, representa el vector 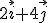 y determina el valor de su módulo y el ángulo que forma con el eje x.
y determina el valor de su módulo y el ángulo que forma con el eje x.
Autoevaluación
Averigua las componentes de un vector 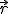 de módulo r = 5 y cuyo ángulo respecto al eje x es
de módulo r = 5 y cuyo ángulo respecto al eje x es 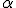 = 53º.
= 53º.
Como sistema de referencia se suele tomar una línea en la dirección del eje x matemático. La posición cero se indica en función de las condiciones de la situación de trabajo. Lo más habitual es que sea la posición de partida del objeto que se mueve.
Pero si el movimiento es vertical se trabaja con el eje y, tomándose como posición cero el suelo, con lo que se evitan posiciones negativas, que son menos intuitivas.
Si el movimiento no es rectilíneo hay que indicar la posición en el plano o en el espacio. Para ello, se eligen los ejes de coordenadas matemáticos tradicionales, x e y, de forma que a la derecha y arriba están las posiciones positivas, y a la izquierda y abajo, las negativas. En este curso solamente llegaremos a estudiar movimientos en el plano.
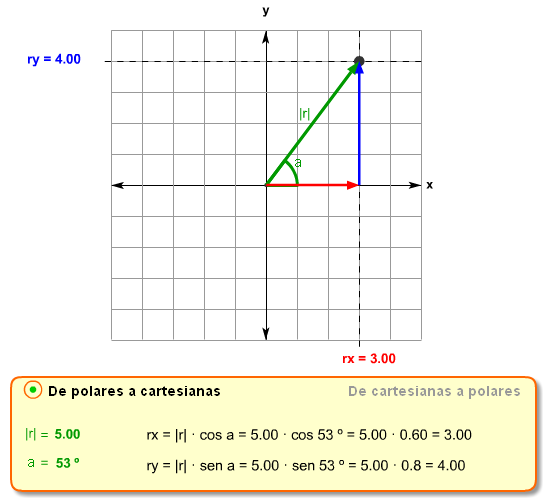
¿Sabes la distancia a la que se lanzan los tiros libres en el baloncesto? ¿Y la altura a la que se encuentra la canasta? Son datos importantes que utilizarás en el tema 4, cuando ya tengas los conocimientos suficientes para resolver el problema del tiro en baloncesto. Determina esos valores a partir del dibujo siguiente, escribiendo el vector de posición de la canasta (coloca el origen de posiciones en el centro de la línea de tiros libres).
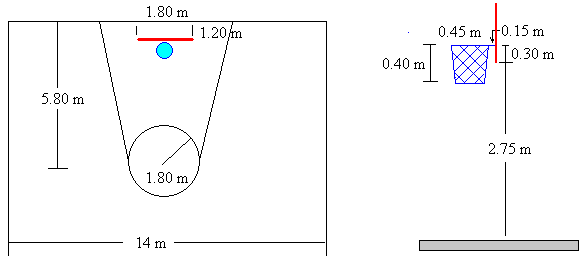
Dibujo de Ángel Franco bajo licencia de uso libre educativo
Verdadero Falso
Verdadero Falso
Verdadero Falso
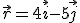 el objeto se encuenta por encima del eje x.
el objeto se encuenta por encima del eje x.
Verdadero Falso