8. Restadores
De modo similar a lo comentado con el sumador, podríamos construir un semi-restador en el que las entradas serán M = minuendo, S = sustraendo, y las salidas D = diferencia, P = cifra prestada. Debe cumplir la siguiente tabla de verdad:
| Entradas | Salidas |
||
| M |
S | D | P |
| 0 | 0 | 0 | 0 |
| 0 |
1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Con lo que sus funciones canónicas serán:
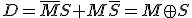
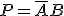
Cuya
posible implementación se muestra en la figura:
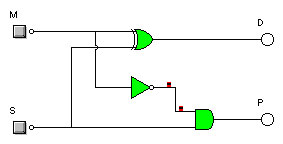 |
| Imagen 27. Elaboración propia |
En
realidad este circuito no existe ya que para realizar restas se emplean
sumadores, puesto que una resta de dos números es igual a la suma de uno con el
negativo del otro. Para lo que se utiliza el método de complemento a uno
(invertir todos los bits uno a uno, es decir cambiando 1 por 0 y 0 por 1), o
bien el método de complemento a dos, añadiéndole un bit de signo. Pero no vamos
a explicar este método de operar
Ni restadores, ni multiplicadores, ni divisores... con sumadores hago de todo!!
Como ya hemos comentado antes, es lo mismo restar, que sumar número de signo opuesto, por lo que no hace falta un restador para la operación resta. Pero, ¿y para multiplicar y dividir?
Lo vemos en un ejemplo muy sencillo,
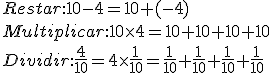
Es decir, con números Reales, podemos sumar, restar, multiplicar y dividir con una sola operación, la suma. Por tanto en cuanto tenemos un sumador, podemos hacer cualquier otra operación sin problemas