1.1.1. Determinación de propiedades

Como hemos dicho, los ensayos simulan las condiciones en que van a trabajar los materiales y de ese modo podemos determinar las características del material y su comportamiento. Por eso de los ensayos debemos sacar unos datos precisos y fiables acerca del material estudiado.

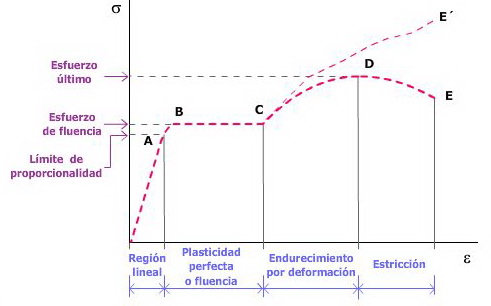
La evaluación del ensayo de tracción se realiza a partir de la curva tensión-deformación, vista en el apartado anterior. Veremos a continuación los parámetros que podemos obtener de ella (tensiones, módulo elástico, deformación...),
Diagrama esfuerzo-deformación
Imagen 16. Elaboración propia.

Analizando desglosadamente las zonas elásticas y plásticas del diagrama anterior, nos encontramos:

El diagrama anterior se pueden clasificar en dos zonas: que son las zonas que un material presenta en cuanto a su comportamiento ante un esfuerzo de tracción:

  • Zona elástica
  • Zona plástica

 


 

 

Icono IDevice Importante

Recuerda: Tensión de tracción (σt)

Para cualquier punto de la gráfica anterior, se calcula como el cociente entre la fuerza de tracción soportada por la probeta y su sección transversal inicial. Se expresa en fuerza por unidad de superficie: Pascales (PA en el Sistema Internacional), o en MPa, o en Kp/cm2.

 

 

 


Zona elástica y plástica en un diagrama esfuerzo-deformación
Imagen 17. Elaboración propia

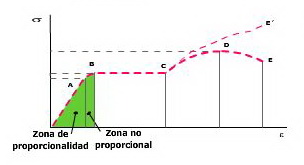
1.- Zona elástica (OB)
Se caracteriza porque al cesar las tensiones aplicadas, los materiales recuperan su longitud inicial. Podemos observar dos subzonas:

 

  • Zona de proporcionalidad (OA)
En la gráfica es una línea recta, es decir, el alargamiento unitario (ε) es proporcional a la tensión ejercida (σ). En las aplicaciones industriales siempre se trabaja en esta zona, ya que no se producen deformaciones permanentes y además se puede aplicar la ley de Hooke.
En esta zona vamos a definir a continuación dos valores importantes:
  • Límite elástico (σE), es la tensión en el límite superior de esta zona; en el punto A
  • El módulo de Young (E)



  • Zona no proporcional (AB) Pequeña zona acontinuación, dónde el material se comporta de forma elástica, pero no existe una relación proporcional entre tensión y deformación.

 

 

 

 

Icono IDevice Importante

Límite elástico (σE)


También se puede definir como la máxima tensión que el material es capaz de soportar sin sufrir deformaciones permanentes.

 

 

 


Esta propiedad juega un papel de gran importancia en el proyecto mecánico, porque las piezas se calculan para que no sufran deformaciones permanentes en servicio y, en consecuencia, se debe garantizar que las tensiones que actúan cuando la pieza trabaja no superan el límite elástico.
Icono IDevice Importante
Modulo de elasticidad o Módulo de Young (E)

 

Es la relación entre la tensión realizada y la deformación que provoca en el tramo lineal de la curva tensión-deformación (región elástica, zona proporcional OA).

Sus unidades son MPa o N/mm2, o bien los Kp/cm2.

También podemos expresarlo como:

 


 

 


2.- Zona plástica (BE)
En esta zona se ha rebasado la tensión del límite elástico y, aunque dejemos de aplicar tensiones de tracción, el material ya no recupera su longitud original y la longitud final será mayor que la inicial "lo".

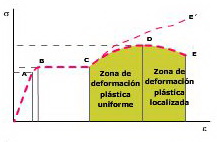
En la zona plástica (BE) también se pueden distinguir tres subzonas:

 

Zonas plásticas en el diagrama esfuerzo-deformación
Imagen 18. Elaboración propia.

  • Zona de deformación plástica uniforme o zona de límite de rotura (CD)
Se consiguen grandes alargamientos con un pequeño incremento de la tensión. En el punto D encontramos el límite de rotura y la tensión en ese punto se llama tensión de rotura (σr). A partir de este punto, la probeta se considera rota, aunque físicamente no lo esté.

  • Zona de rotura o zona de estricción o zona de deformación plástica localizada (DE)
Las deformaciones son localizadas y, aunque disminuya la tensión, el material se deforma hasta la rotura. La sección de la probeta se reduce drásticamente.

 

Icono IDevice Objetivos
En el caso del acero existe una zona justo al sobrepasar el límite elástico, ya en la Zona Plástica, en el que se da una deformación apreciable sin que varíe la tensión aplicada. Este fenómeno se denomina fluencia y la tensión en ese punto se denomina tensión de fluencia (σF).
Se trata de la zona BC del diagrama anterior.
Zona de fluencia
Imagen 19. Elaboración propia.


Icono IDevice Importante

Tensión de tracción a rotura (σR)

Es la tensión de tracción soportada por la probeta en el punto "D", que es en la gráfica anterior es el valor máximo de tensión que soporta la probeta.

 


 

 


En general, los metales y aleaciones muestran una relación lineal entre la tensión y la deformación en la región elástica en un diagrama tensión–deformación que se describe mediante la ley de Hooke.

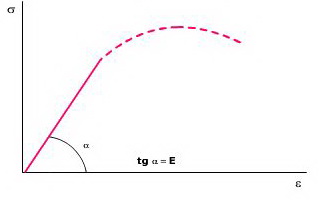
El módulo de elasticidad resulta ser igual, pues, a la tangente de la recta de la gráfica en su zona de proporcionalidad. Vemos que en esa región del diagrama tensión–deformación el módulo de elasticidad no cambia al aumentar la tensión.

El módulo de elasticidad como pendiente de la curva esfuerzo-deformación
Imagen 20. Elaboración propia.

Si comparamos las gráficas de un material dúctil (Límite elástico (σE) más bajo pero se estira más) y un material frágil (Límite elástico (σE) más alto, pero se estira menos).


Imagen 21. Elaboración propia.



Icono IDevice Para saber más

Coeficiente de seguridad (n)

Para garantizar que un material va a trabajar en la zona elástica, se aplica un coeficiente de seguridad, de modo que la tensión de trabajo σt siempre debe ser inferior a la tensión del límite elástico σE.

Se calcula según la fórmula:

 

 


Icono IDevice Objetivos

A continuación tienes un Video Tutorial, sobre el Ensayo de Tracción, procedente del catálogo de la Universidad Politécnica de Valencia

 

Imagen 22. Elaboración propia.

 

 


Icono de iDevice Ejemplo o ejercicio resuelto

Resuelve este ejercicio en el que debes calcular algunas de las propiedades vistas a partir de un ensayo de tracción.

Presta atención especial a las unidades.

 

 

En el gráfico adjunto se muestra la curva fuerza-incremento de longitud, resultante del ensayo de tracción de un material polimérico.
Curva fuerza-incremento de longitud en un ensayo
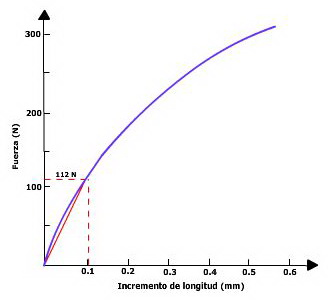DATOS DEL ENSAYO:
  • Dimensiones de la probeta
  • Anchura: 12.61 mm
  • Espesor: 3.47 mm
  • Longitud inicial: 50 mm
  • Longitud final después de la rotura: 97 mm.
  • Fuerza máxima alcanzada en el ensayo: 1290 N.

Imagen 23 . Elaboración propia.
  
Calcular:
a) Módulo de Elasticidad o de Young (GPa).
b) Resistencia a la Tracción (MPa).
c) %Alargamiento a la rotura (ε)

Icono IDevice Para saber más

En esta dirección encontrarás un glosario en el que aparecen todos los términos relativos a la resistencia de los materiales: ensayos, deformaciones…, glosario que te puede aclarar algún concepto que no te haya quedado lo suficientemente claro.


http://www.instron.com.es/wa/resourcecenter/glossary.aspx


« Anterior | Siguiente »