1.1. En el medio
 |
| Imagen de Iowapolitics.com con licencia Creative Commons |
Nuestra empresa TisBet Survey ha recibido el encargo de realizar un estudio sobre el nivel de aceptación de un determinado líder político. A cada una de las 600 personas consultadas se le pidió que asignara una calificación con un número natural de 0 a 10, obteniéndose los siguientes resultados.
| Puntuación | 0 | 1 | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| N.º de personas |
12 |
38 | 62 | 97 | 160 | 130 |
65 |
18 |
11 |
6 |
1 |
La aceptación media del líder vendrá dada por la suma de todas las puntuaciones obtenidas dividida por las 600 opiniones.
Para el cálculo de la aceptación media nos ayudaremos de la construcción de la siguiente tabla, donde:
La primera columna es el valor de los posibles valores de la variable.
La segunda columna es la frecuencia absoluta de cada valor, es decir, el número de encuestados que han respondido un valor determinado.
Cada celda de la tercera columna corresponde al producto de las celdas, que están en la misma fila, de las dos primeras columnas.
| xi | fi |
xi·fi |
| 0 | 12 |
0·12=0 |
| 1 |
38 | 1·38=38 |
| 2 |
62 |
2·62=124 |
| 3 |
97 |
291 |
| 4 |
160 |
640 |
| 5 |
130 |
650 |
| 6 |
65 | 390 |
| 7 |
18 |
126 |
| 8 |
11 | 88 |
| 9 |
6 | 54 |
| 10 |
1 | 10 |
| N=600 |
2411 |
En la última fila calcularemos la suma de todos los elementos de esa columna. Así, en la columna fi la suma corresponderá con el número de personas entrevistadas. En la columna xi·fi sumamos cada valor multiplicado por el número de personas que lo han elegido, esto corresponde a la suma de todas las calificaciones obtenidas.
La aceptación media de este líder vendrá dada por la media aritmética de estos resultados. Es decir, el cociente entre la suma de todas las calificaciones obtenidas, 2411 (última fila, tercera columna) y el número de personas encuestadas, 600 (que se corresponde con la suma de los valores de la segunda columna).
Importante
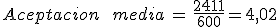
Se llama Media Muestral (Media aritmética) de una variable estadística al cociente entre la suma de todos los valores obtenidos en la muestra y el tamaño de la muestra. La media muestral se representa por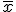 
. Recuerda que la media poblacional se representa por la letra griega μ
Si X es una variable estadística que toma los valores x1, x2, x3, ..... xn con frecuencias absolutas f1, f2, f3, ..... fn , respectivamente, la media de la variable X viene dada por la siguiente expresión:
Ejemplo o ejercicio resuelto
 |
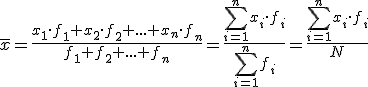
| Imagen de pointshoot con licencia Creative Commons |
Se está haciendo un estudio sobre alimentación y sobrepeso en adolescentes. Para ello se ha escogido a una muestra de 25 personas de entre 15 y 16 años que son clientes habituales de locales de comida rápida. Los datos sobre el peso en kilogramos obtenidos son los siguientes:
| 49,5 |
57,0 |
65,0 |
60,0 |
74,5 |
47,0 |
50,6 | 49,5 |
64,3 |
| 45,2 |
48,4 |
58,1 |
66,5 |
76,1 |
48,8 |
56,2 | 66,5 |
77,0 |
| 41,0 | 46,0 | 54,2 |
63,8 |
46,0 |
51,5 |
68,2 |
Divide la población en 6 intervalos de clase de longitud 6 y halla el peso medio de esta muestra.
AV - Reflexión
En la escena siguiente elaborada por Miguel Ángel Cabezón Ochoa en Descartes puedes practicar el cálculo de la media. Hay ejercicios de variable continua y discreta mezclados.
Objetivos
La media arítmetica no es la única media que podemos calcular. Hay una variación de esta en la que a cada valor se le da un peso. A esta media se le llama Media ponderada.
La otra media en la que en vez de sumar se multiplica se llama Media geométrica.