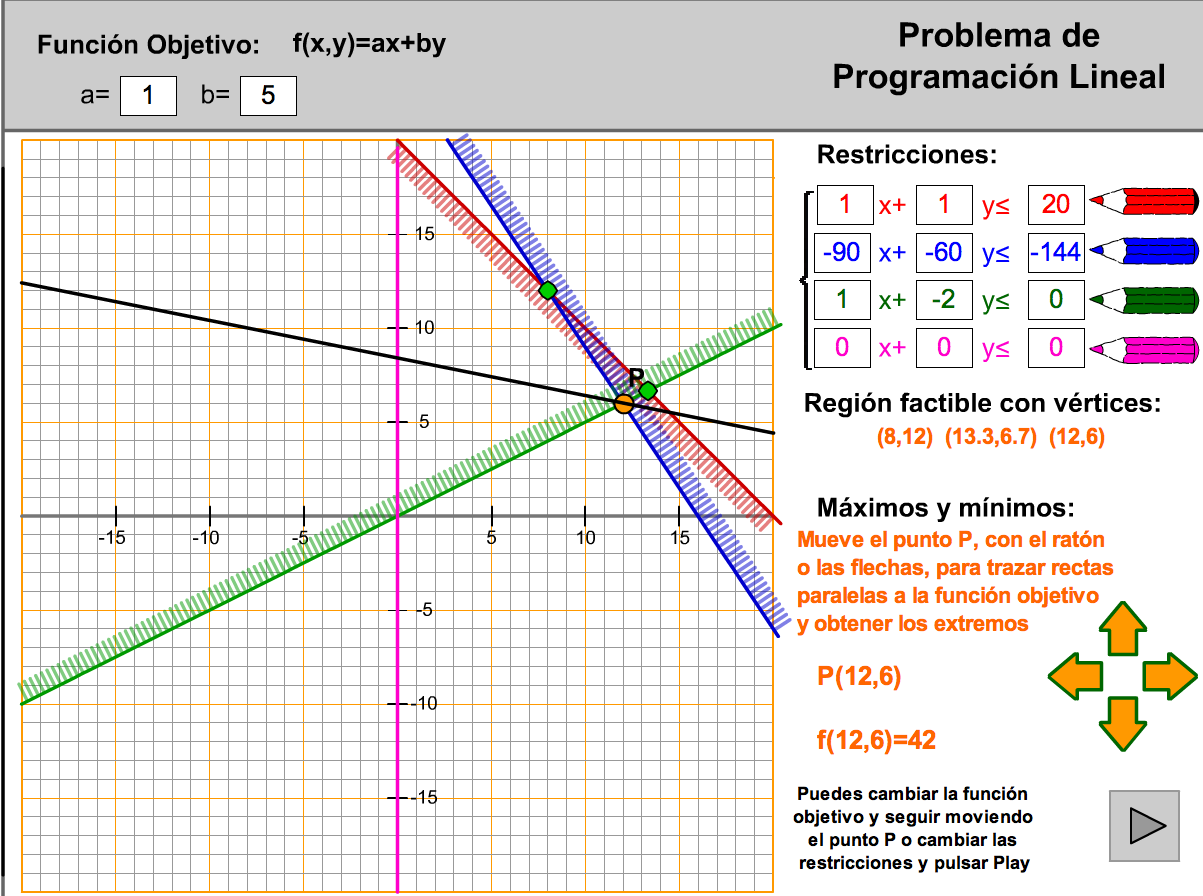
1.3. Lo resolvemos
Para encontrar la solución nos vamos a ayudar de la función objetivo F(x,y)=120x+60y. ¿Cómo?, representando en primer lugar la recta 120x+60y=0, y a partir de ella iremos trazando rectas paralelas hasta que lleguemos a la región factible.
Recuerda que todas las rectas que son paralelas a 120x+60y=0 son aquellas que tienen la forma 120x+60y=k, donde k puede tomar cualquier valor.
Vamos a verlo gráficamente. Para ello, en la siguiente escena, mueve el punto k, que está sobre el deslizador rojo. Llévalo a cero y aumenta su valor hasta que topes con el primer punto factible. Este punto será la solución de nuestro problema.
|
|
Imagen de Wikimedia Commons con licencia Creative Commons
|
Para este punto la función objetivo toma un valor de 1320, es decir, F(6,10)=120·6+60·10=720+600=1320. El coste de enviar las furgonetas es de 1320€.
Conclusión:
Tenemos que enviar 6 furgonetas del Tipo I y 10 furgonetas del tipo II. El coste de la operación es de 1320€.
Después de ver el resultado parece lógico pensar que tenemos que enviar el mayor número de furgonetas del tipo II disponibles, ya que su coste es justo la mitad de las del tipo I y dos furgonetas del tipo II(coste 120€) transportan 60 paquetes, 10 más que una sola del tipo I (coste 120€). Es decir, a igual coste es mejor enviar 2 del tipo II, que una del tipo I.
Con este vídeo podrás repasar todo el proceso de construcción de un problema de programación lineal a partir del planteamiento del problema. Pertenece a una serie llamada Programación lineal que consta de 11 videos, te pueden ser de gran ayuda:
Importante
- La solución para un problema de programación lineal, si existe, siempre se alcanzan en los vértices de la región factible.
- Si el valor óptimo se alcanza en dos de los vértices de la región factible A y B, entonces también son solución todos los puntos del segmento AB, es decir, el que corresponde a un lado de la región factible.
Ejemplo o ejercicio resuelto
 |
|
Animación del Banco de imágenes y sonidos del ITE
bajo
licencia Creative Commons
|
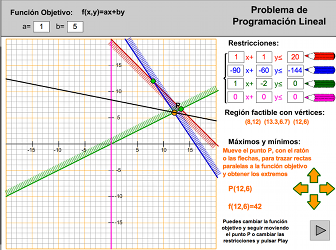
Bueno, vamos a terminar el problema de las bombillas. Para ello puedes ayudarte de una herramienta (haz clic en la imagen) que resuelve problemas de programación lineal una vez que los tenemos planteados.
Sólo tenemos que escribir los coeficientes de la función objetivo y de las restricciones (cómo máximo admite 4 restricciones)
Vamos pulsando el botón que hay en la parte inferior derecha y vemos como se van dibujando cada una de las restricciones y la función objetivo.
Una vez que termina la representación puedes mover el punto amarillo con el ratón o con los cursores que hay en la parte inferior derecha.
Justo al lado de los cursores está el punto representado y el valor de la función objetivo para ese punto.
Te recuerdo que el valor óptimo, si existe, está en los vértices de la región factible.
AV - Pregunta de Elección Múltiple|
Encontrar unas restricciones
| |
|
Representar una región factible
| |
|
Optimizar una función objetivo sujeta a unas restricciones
| |
|
Calcular el valor mínimo de una función a partir de una región factible
|
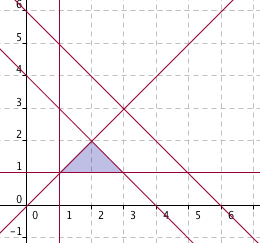
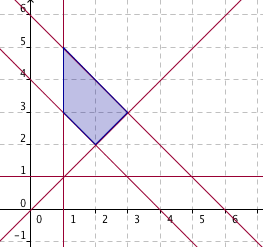
2. La región factible determinada por las restricciones:
2x+2y≤8
x+y≤6
y≥x
x≥1, y≥1
es una de las siguientes:
 |
 |
 |
 |
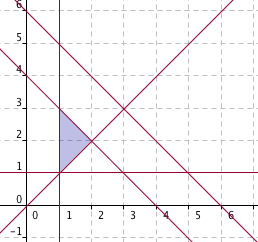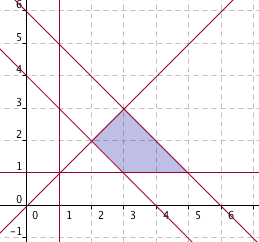| Región 1 |
Región 2 |
Región 3 |
Región 4 |
|
Región 1
| |
|
Región 2
| |
|
Región 3
| |
|
Región 4
|
3. La siguiente imagen representa la región factible de un problema de programación lineal, junto con una de las representaciones de la función objetivo F(x,y).
 |
|
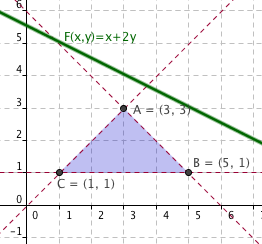El valor mínimo de la función objetivo se alcanza en el punto B(5,1)
| |
|
El valor máximo de la función objetivo se alcanza en cualquier punto del segmento AB
| |
|
El valor mínimo de la función objetivo se alcanza en el punto (3,2)
| |
|
El valor mínimo de la función objetivo se alcanza en el punto C(1,1)
|