2.2. Probando el metro
 |
| Edificio. Imagen obtenida del Banco de imágenes del ITE. |
Un arquitecto ha diseñado un edificio cuya fachada se adapta a la gráfica de la función
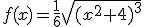 en el intervalo
en el intervalo 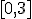 medido en cientos de metros.
medido en cientos de metros.
Una vez construido el edificio deben instalar un tubo de agua que recorra toda la fachada del edificio por motivos de seguridad para la prevención de posibles incendios. El tubo debe estar situado a 5 metros del suelo.
Ayuda a los bomberos a calcular la longitud que tendrá ese tubo para saber la presión con la que tendrán que bombear el agua por el mismo en caso de que ocurra un incendio.
Uno de los cortes transversales de la supercicie que aparece en la ventana interactiva inferior sigue la función
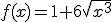 en el intervalo
en el intervalo 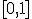
La gráfica de esta función es:
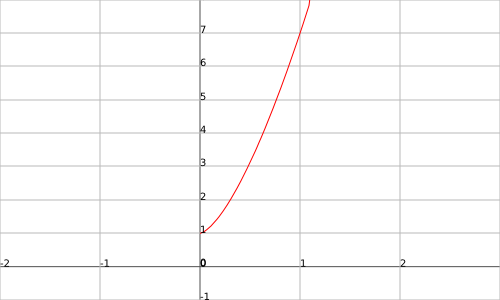 |
Calcula su longitud.
Calcula las siguientes medidas:
a) Longitud del arco de curva 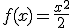 en el intervalo
en el intervalo 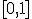 .
.
b) Longitud del arco de curva 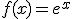 en el intervalo
en el intervalo 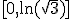
Calcula la longitud de la curva
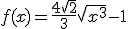 en el intervalo
en el intervalo 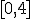
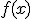 en el intervalo
en el intervalo 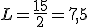 medido en cientos de metros, según nos indicaron. entonces tenemos que la longitud del tubo es
medido en cientos de metros, según nos indicaron. entonces tenemos que la longitud del tubo es
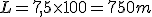
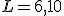
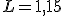 .
.
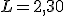 .
.
