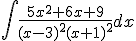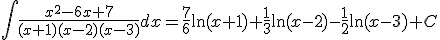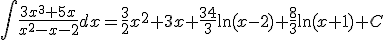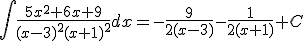2.3. De forma racional
En el caso de tener que realizar una integral de la forma
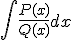 donde
donde 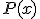 y
y 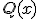 son funciones polinómicas. En este caso, vamos a intentar descomponer el anterior cociente de funciones polinómicas en fracciones más sencillas.
son funciones polinómicas. En este caso, vamos a intentar descomponer el anterior cociente de funciones polinómicas en fracciones más sencillas.
Si el grado del polinomio 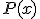 es mayor que el grado del polinomio
es mayor que el grado del polinomio 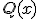 , podemos hacer la división efectiva y tendremos que
, podemos hacer la división efectiva y tendremos que
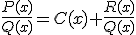 donde
donde 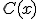 y
y 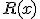 son funciones polinómicas, cumpliéndose que el grado de
son funciones polinómicas, cumpliéndose que el grado de 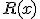 es menor que el de
es menor que el de 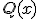 . Así, tenemos que
. Así, tenemos que
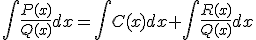
En la siguiente ventana interactiva encontrarás información de cómo debemos abordar este tipo de integrales. Pulsa sobre ella para seguir avanzando:
|
|
Calcula la siguiente integral 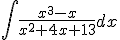
|
|
Dada la siguiente función 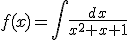
represéntala gráficamente en la siguiente ventana, sabiendo que la constante que resulta de la integral es 1.
|
Applet interactiva obtenida de la aplicación "Patrimonio Matemático de los Pueblos" de Mariano Real Pérez. Contenido interactivo del ITE. Para obtener un manual detallado pulsa aquí |
Representa gráficamente la siguiente función en la ventana interactiva anterior:
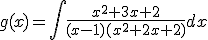
Sabiendo que la constante es 0.
Calcula las siguientes integrales:
a) 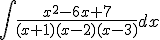
b) 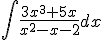
c)