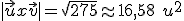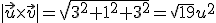1.3. Midiendo áreas con vectores
Desde hace mucho tiempo conoces ciertas expresiones ó fórmulas para calcular áreas. La expresión que determina el área de un cuadrado en función de su lado, 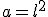 , es una de las primeras expresiones que se se suelen conocer en la escuela primaria. Asi mismo, para calcular el area de un paralelogramo en función de su base y su altura podemos utilizar
, es una de las primeras expresiones que se se suelen conocer en la escuela primaria. Asi mismo, para calcular el area de un paralelogramo en función de su base y su altura podemos utilizar 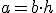 .
.
Si nos planteamos calcular el área de un paralelogramo, nos encontramos con que podemos averiguar el valor de h:
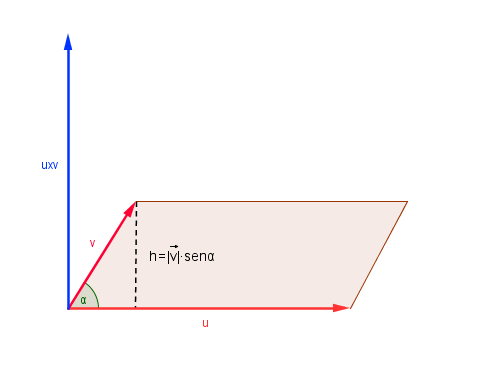
El área sombreada del paralelogramo formado por los vectores 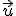 y
y 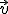 es
es
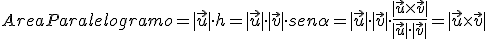
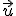 = (-1,-1,8) y
= (-1,-1,8) y 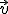 = (2,1,-1)
= (2,1,-1)
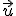 = (1,0,-1) y
= (1,0,-1) y 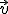 = (-2,3,1)
= (-2,3,1)
En el siguiente applets de Descartes, puedes apreciar la representación gráfica de dos vectores y el cálculo del área del paralelogramo formados por ellos.
El applet, creado por Consolación Ruiz Gil, se encuentra bajo una licencia Creative Commons.
El área del triángulo formado por dos vectores 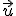 y
y 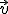 es la mitad del módulo del producto vectorial.
es la mitad del módulo del producto vectorial.
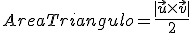
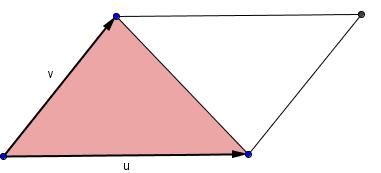
Como consecuencia, para hallar el área de un triángulo, conociendo sus tres vértices, basta construir dos vectores sobre esos tres puntos y al área es la mitad del módulo del producto vectorial de esos dos vectores. En la parte de P.A.U. tienes algún ejemplo.
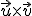
 (2,1,-1) = (-7,15,1)
(2,1,-1) = (-7,15,1)