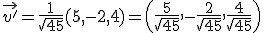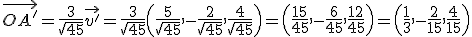2.1. Así nos transformamos
|
|
Si tenemos dos vectores 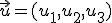 y
y 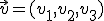 vamos a llamar producto escalar de los dos vectores anteriores al número:
vamos a llamar producto escalar de los dos vectores anteriores al número:
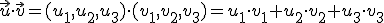
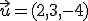 y
y 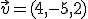
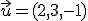 y
y 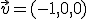 . El producto escalar es
. El producto escalar es
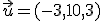 y
y 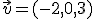 . El producto escalar es
. El producto escalar es
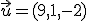 y
y 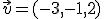 . El producto escalar es
. El producto escalar es
 |
Además, se tiene que dados dos vectores 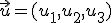 y
y 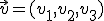 , se cumple que
, se cumple que
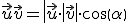
Donde 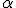 es el ángulo que forma
es el ángulo que forma 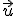 con
con 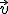
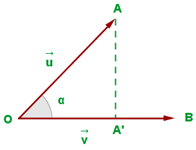
Utilizando la trigonometría, según la imagen que observamos en la parte de la derecha, sabemos que la proyección del vector 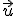 sobre el vector
sobre el vector 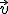 es:
es:
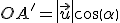
Por tanto, el producto escalar del vector 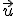 y el vector
y el vector 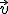 es el resultado de multiplicar la proyección del vector
es el resultado de multiplicar la proyección del vector 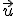 sobre el vector
sobre el vector 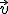 , por el módulo del vector
, por el módulo del vector 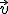 .
.
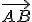 y
y 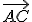 es lo mismo que el producto de
es lo mismo que el producto de 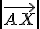 (proyección de
(proyección de 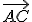 sobre
sobre 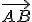 ) por
) por 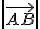 . Esto nos da la oportunidad de calcular la longitud de esa proyección con una sencilla operación de dividir. También nos da la posibilidad de conocer el ángulo que forman los dos vectores despejando.
. Esto nos da la oportunidad de calcular la longitud de esa proyección con una sencilla operación de dividir. También nos da la posibilidad de conocer el ángulo que forman los dos vectores despejando.
Calcula el vector proyección del vector 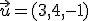 sobre el vector
sobre el vector 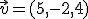 .
.
Ayúdate de la imagen del Importante.
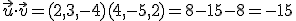
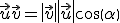
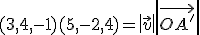
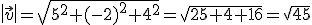
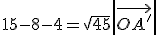
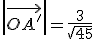 que es la longitud de la proyección. Para calcular el vector proyección, es decir, el vector
que es la longitud de la proyección. Para calcular el vector proyección, es decir, el vector 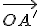 calculamos un vector unitario de la misma dirección y sentido que el vector
calculamos un vector unitario de la misma dirección y sentido que el vector