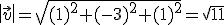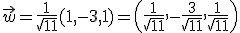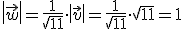1.2. Un sastre para la familia
 |
| Metro. Imagen obtenida del banco de imágenes del ITE. |
Cuando tenemos una medida de longitud la expresamos en función de una unidad de medida, por ejemplo el metro. Igual sucede con una medida de área que por ejemplo la expresamos en metros cuadrados.
En el caso de los vectores vamos a buscar las "unidades" correspondientes.
Importante
Cuando un vector tiene módulo 1 se denomina vector unitario. Ya conoces algunos de estos vectores unitarios: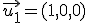 
, 
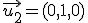y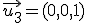 
. A partir de estos tres vectores unitarios tenemos que un vector cualquiera, por ejemplo 
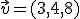lo podemos expresar como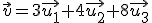 
Además de estos vectores unitarios, podemos conseguir muchísimos más. ¿Cómo? en el siguiente ejemplo te lo aclaramos:
|
|
Ejemplo o ejercicio resuelto
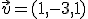, es decir, un vector que tenga la misma dirección y el mismo sentido, pero que su módulo sea 1.
AV - Pregunta de Elección Múltiple
| |
| |
| |
|
Curiosidad
 |
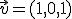
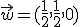
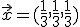
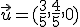
Hermann Grassmann era el tercero de los doce hijos de Justus Günter Grassmann y Johanne Luise Friederike Medenwald. Su madre era hija de un pastor de Klein-Schönfeld. Su padre también había sido consagrado pastor, pero consiguió una plaza de profesor de matemáticas y física en el Instituto de Stettin. Fue un académico notable, autor de libros de texto escolar de Física y Matemáticas, y llevó a cabo investigaciones en el campo de la cristalografía. Otro hermano de Hermann, Robert, también se dedicó a las matemáticas y ambos trabajaron conjuntamente en muchos proyectos.
Entre otros temas, Grassman realizó un ensayo sobre la teoría de las mareas. Lo elaboró en 1840, tomando como base la teoría de la Méchanique analytique de Lagrange y de la Méchanique céleste de Laplace, pero exponiendo esta teoría por métodos vectoriales, sobre los que trabajaba desde 1832. Este ensayo, publicado por primera en los Collected Works de 1894-1911, contiene el primer testimonio escrito de lo que hoy se conoce como álgebra lineal y la noción de espacio vectorial.
En 1844, Grassmann publica su obra maestra, Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik, más conocido como Ausdehnungslehre, que se puede traducir como "teoría de la extensión" o "teoría de las magnitudes extensivas". Después de proponer en ella nuevas bases para todas las matemáticas, el trabajo empieza con definiciones de naturaleza más bien filosófica. Grassmann demostró además que si la geometría se hubiese expresado en forma algebraica como él proponía, el número tres no hubiese desempeñado el papel privilegiado que tiene como número que expresa las dimensiones espaciales; de hecho, el número de posibles dimensiones de interés para la geometría es ilimitado.
La idea puede parecernos ahora simple, pero en aquella época suponía un auténtico golpe de audacia. El planteamiento era (y sigue siendo) el siguiente: Grassmann define unos “vectores línea” (Strecke) que tienen módulo unidad y están situados en los ejes de coordenadas. Por ejemplo, en el plano se tienen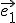 
y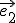 
el primero sobre el eje X y el segundo sobre el eje Y, de forma que el vector (2, 3) es la suma vectorial de dos veces el primero más tres veces el segundo:
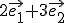
Se trabajaría análogamente en tres dimensiones, donde un vector cualquiera como (3, -2, 1) vendría representado como:
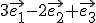
Por todo ello H. G. Grassmann está considerado como el fundador del Cálculo Vectorial.