1.1. Así medimos a los vectores
Dado un vector cualquiera 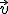 , el módulo de este vector es su longitud, es decir, lo que mide. Si el vector
, el módulo de este vector es su longitud, es decir, lo que mide. Si el vector 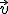 tiene como coordenadas
tiene como coordenadas 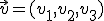 sabemos que el vector es el mismo que el vector que va del origen de coordenadas
sabemos que el vector es el mismo que el vector que va del origen de coordenadas 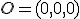 al punto
al punto 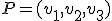 , por tanto, la longitud del vector
, por tanto, la longitud del vector 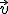 es la distancia del punto
es la distancia del punto 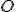 al punto
al punto 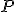 .
.
El módulo del vector 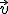 lo escribimos
lo escribimos 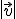 . Con todo lo anterior tenemos que:
. Con todo lo anterior tenemos que:
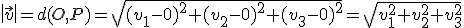
En la siguiente ventana puedes mover el vector que aparece y comprobarás el módulo que tiene:
Instrucciones:
- Arrastre el ratón para rotar la figura.
- Arrastre la punta del vector. Puede también arrastrar las coordenadas x, y, z del vector.
- En la punta del vector aparece su módulo
- Shift + arrastre vertical = zoom
La fuerza de atracción 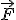 entre un objeto de masa
entre un objeto de masa 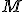 y otro de masa
y otro de masa 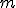 , cuando una distancia
, cuando una distancia  separa los centros de ambos viene dada por la fórmula:
separa los centros de ambos viene dada por la fórmula:
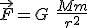
La constante universal G fue medida por Cavendish utilizando un experimento en función del ángulo que gira el hilo que une dos cuerpos, en función de lo cerca que estén los cuerpos. La fuerza es un vector cuyo módulo se calcula según la fórmula anterior. La dirección y el sentido serían la recta que une el centro de ambos cuerpos y desde el más pequeño al más grande.
1.- El módulo del vector 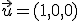 es
.
es
.
2.- El módulo del vector 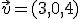 es
.
es
.
3.- El módulo del vector 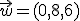 es
.
es
.
El módulo de un vector cumple las siguientes propiedades:
Si tenemos dos vectores 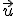 y
y 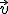 y dado un número cualquiera positivo
y dado un número cualquiera positivo  tenemos que:
tenemos que:
1.- Si 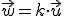 entonces
entonces 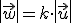
2.- 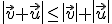 Esta última propiedad es muy sencilla de ver ya que al contruir gráficamente la suma de dos vectores nos resulta un triángulo y lo que la propiedad indica es que uno de los lados de ese triángulo es menor que la suma de los otros dos.
Esta última propiedad es muy sencilla de ver ya que al contruir gráficamente la suma de dos vectores nos resulta un triángulo y lo que la propiedad indica es que uno de los lados de ese triángulo es menor que la suma de los otros dos.
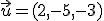 ,
, 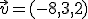 y el número
y el número 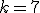 , comprueba que se cumplen las dos propiedades anteriores.
, comprueba que se cumplen las dos propiedades anteriores.