3.1 Ejercicios
¿Son  ,
,  y
y  una base de
una base de 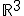 ?
?
Si  son linealmente independientes, ¿forman los vectores
son linealmente independientes, ¿forman los vectores  ,
,  y
y  una base de
una base de 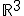 ?
?
Sean los vectores (1,0,0) y (1,1,0).
Probar que son linealmente independientes.
Encontrar un vector  que sea combinación lineal de los anteriores y perpendicular a (1,0,0)
que sea combinación lineal de los anteriores y perpendicular a (1,0,0)
En 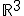 , sean los vectores
, sean los vectores
 y
y 
a)¿Para qué valores de m son linealmente dependientes?
b)Determinar en tal caso 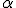 y
y  de modo que
de modo que 
Demuestra que si  es una base de
es una base de 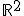 entonces
entonces  también es una base.
también es una base.
 es una base de
es una base de 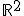 entonces
entonces  también es una base.
también es una base.
a) Determinar un valor de p para que los vectores  ,
,  y
y  sean linealmente dependientes.
sean linealmente dependientes.
b) Para el valor de obtenido, hallar una relación de dependencia lineal entre esos vectores.
obtenido, hallar una relación de dependencia lineal entre esos vectores.
 ,
,  y
y  sean linealmente dependientes.
sean linealmente dependientes.b) Para el valor de
 obtenido, hallar una relación de dependencia lineal entre esos vectores.
obtenido, hallar una relación de dependencia lineal entre esos vectores.
Determina un vector 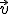 de
de 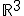 sabiendo que cumple las tres siguientes condiciones:
sabiendo que cumple las tres siguientes condiciones:
1.- La suma de sus tres coordenadas es 3.
2.- 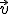 es combinación lineal de
es combinación lineal de  y
y 
3.- Los vectores (1,0,1), (0,1,0) y 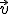 son linealmente dependientes
son linealmente dependientes
 y
y  forman una base de
forman una base de  solamente tiene una solución que es
solamente tiene una solución que es  . Por tanto vamos a ver si esto es así:
. Por tanto vamos a ver si esto es así:





 es una base de
es una base de 






 resolviendo tenenmos que
resolviendo tenenmos que 


 tenemos los vectores
tenemos los vectores  ,
,  y
y  . Para conocer la relación de dependencia lineal hacemos:
. Para conocer la relación de dependencia lineal hacemos:
 de donde tenemos que
de donde tenemos que




 tenemos los vectores
tenemos los vectores  ,
,  y
y  . Para conocer la relación de dependencia lineal hacemos:
. Para conocer la relación de dependencia lineal hacemos:
 de donde tenemos que
de donde tenemos que




