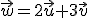2.2¿Me puede decir dónde estoy?
 |
Imagina la siguiente situación: Vas en el asiento de atrás de un coche que circula a una velocidad 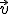 y lanzas un papel hacia adelante a una velocidad
y lanzas un papel hacia adelante a una velocidad  . ¿A qué velocidad observas que se mueve el papel?.... Evidentemente, a la velocidad
. ¿A qué velocidad observas que se mueve el papel?.... Evidentemente, a la velocidad  .
.
Si una persona que está parada en la carretera observa toda la escena, dirá que el papel va a una velocidad 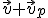 .
Con este ejemplo parece claro que necesitamos una referencia, una base
respecto a la que calcular los vectores que manejamos. El sistema de
referencia que utilizas cuando estás dentro del coche es distinto del
sistema de referencia que utiliza la persona que está parada en la
carretera.
.
Con este ejemplo parece claro que necesitamos una referencia, una base
respecto a la que calcular los vectores que manejamos. El sistema de
referencia que utilizas cuando estás dentro del coche es distinto del
sistema de referencia que utiliza la persona que está parada en la
carretera.
Podemos complicar un poco más la situación. Imagina que un astronauta que está en un satélite que siempre se mantiene a la misma distancia de la Tierra observa el lanzamiento del papel. En este caso, este astronauta observa que la velocidad a la que se mueve el papel es la suma de las dos anteriores más la de rotación de la Tierra.
Si alguien estuviera en el Sol y observara el lanzamiento del papel, observaría que la velocidad a la que se mueve es la suma de las tres anteriores más la de traslación de la Tierra.
¿No te da vértigo pensar la velocidad a la que viajamos cuando estamos parados?
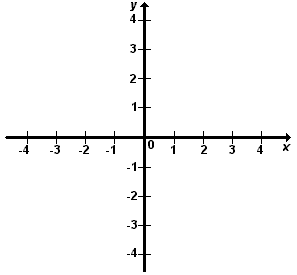 |
Así, para trabajar con vectores lo primero que debemos tener determinado es un sistema de referencia. En el caso del plano, 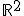 ya conoces el sistema de referencia que aparece en la imagen de la
derecha. En este sistema observamos dos vectores que vamos a destacar:
ya conoces el sistema de referencia que aparece en la imagen de la
derecha. En este sistema observamos dos vectores que vamos a destacar:
.- El primero es el que une el punto (0,0) con el punto (1,0): 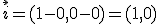 .
.
.- El segundo es el que une el punto (0,0) con el punto (0,1):  .
.
Estos dos vectores son linealmente independientes y cualquier vector
del plano lo vamos a poder poner como combinación lineal de estos dos.
Por ejemplo, si consideramos el vector 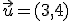 tenemos que
tenemos que 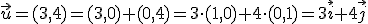
Así decimos que los vectores  y
y 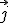 son una base de
son una base de 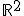
 |
En el caso de 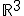 ya hemos trabajado con el sistema de referencia que aparece en la imagen de la derecha. Ahí podemos ver representado el punto
ya hemos trabajado con el sistema de referencia que aparece en la imagen de la derecha. Ahí podemos ver representado el punto 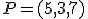 . en este sistema de referencia observamos tres vectores que vamos a destacar:
. en este sistema de referencia observamos tres vectores que vamos a destacar:
.- El primero es el que une el punto (0,0,0) con el punto (1,0,0): 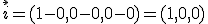 .
.
.- El segundo es el que une el punto (0,0,0) con el punto (0,1,0): 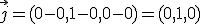 .
.
.- El tercero es el que une el punto (0,0,0) con el punto (0,0,1): 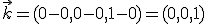 .
.
Estos tres vectores son linealmente independientes y cualquier vector del espacio lo vamos a poder poner como combinación lineal de estos tres.
Por ejemplo, si consideramos el vector  . Tenemos que
. Tenemos que

Así decimos que los vectores  ,
, 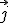 y
y 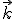 son una base de
son una base de 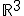
 |
| Hito topográfico de las tres fronteras. Imagen obtenida del banco de imágenes del ITE |
A nivel de la Tierra también nos encontramos con problemas similares a
los que vimos en el ejemplo del lanzamiento del papel en el coche, pero
no te preocupes que ya han sido solucionados. El problema es encontrar
un sistema de referencia para resolver los problemas vectoriales que
tengamos y poder tomar medidas reales. Así, en el espacio 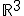 no siempre vamos a poder encontrar una base tan sencilla como la
anterior ya que vamos a tener que basarla en puntos que conozcamos. Un
ejemplo claro de este caso lo tenemos en los puntos de referencia que
utilizan los topógrafos. Los hitos como el que podemos observar en la
imagen de la derecha. Con tres de estos hitos: A, B y C tenemos una
base vectorial formada por los tres vectores
no siempre vamos a poder encontrar una base tan sencilla como la
anterior ya que vamos a tener que basarla en puntos que conozcamos. Un
ejemplo claro de este caso lo tenemos en los puntos de referencia que
utilizan los topógrafos. Los hitos como el que podemos observar en la
imagen de la derecha. Con tres de estos hitos: A, B y C tenemos una
base vectorial formada por los tres vectores 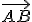 ,
,  y
y 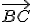 , pero la combinación lineal no va a resultar tan fácil como la que hemos observado anteriormente con el vector
, pero la combinación lineal no va a resultar tan fácil como la que hemos observado anteriormente con el vector 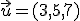 .
A partir de este tipo de bases generan los distintos mapas topográficos
que después sirven para la realización de carreteras, explotaciones
mineras, movimientos de tierras, etc. Estos mismos mapas son los
utilizados por el ejército. En el Instituto Geográfico Nacional aparecen recopilados.
.
A partir de este tipo de bases generan los distintos mapas topográficos
que después sirven para la realización de carreteras, explotaciones
mineras, movimientos de tierras, etc. Estos mismos mapas son los
utilizados por el ejército. En el Instituto Geográfico Nacional aparecen recopilados.
En un espacio vectorial, una base va a venir determinada por el mayor número de vectores linealmente independientes. Este número de vectores será la dimensión del espacio vectorial.
Así, en el espacio vectorial 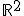 una base vendrá dada por dos vectores linealmente independientes ya que este espacio es de dos dimensiones. Una base de
una base vendrá dada por dos vectores linealmente independientes ya que este espacio es de dos dimensiones. Una base de 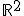 ya la conocemos, es la compuesta por los vectores
ya la conocemos, es la compuesta por los vectores 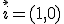 y
y 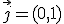 .
.
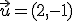 y
y 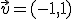 forman una base de
forman una base de 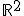 y escribe el vector
y escribe el vector  como combinación lineal de los dos primeros
como combinación lineal de los dos primeros
En el espacio vectorial 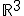 una base vendrá dada por
vectores linealmente independientes ya que este espacio es de
dimensiones. Una base de
una base vendrá dada por
vectores linealmente independientes ya que este espacio es de
dimensiones. Una base de 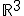 ya la conocemos, es la compuesta por los vectores
ya la conocemos, es la compuesta por los vectores 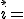 ,
, 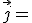 y
y 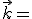 .
.
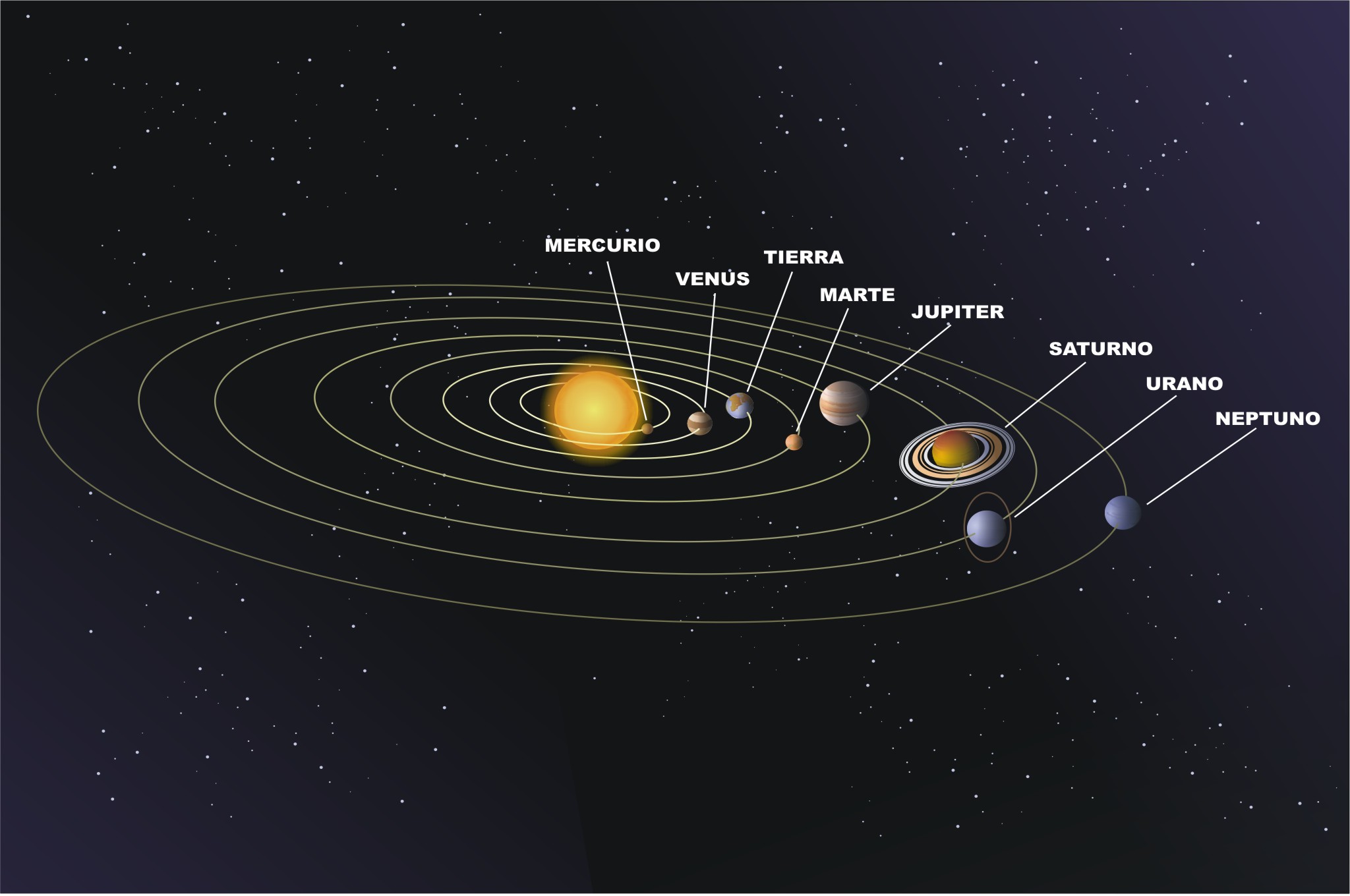 |
| Sistema Solar. Imagen obtenida del Banco de imágenes del ITE |
¿Recuerdas a Darío? ¿Que siembre debía estar atento a los asteroides y
los movimientos que se producían en el Universo?. Pues para hacer su
trabajo hoy, ha establecido una base del espacio vectorial para el
Sistema Solar basándose en las posiciones del Sol, Saturno y Urano,
obteniendo respectivamente los vectores 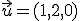 (vector Tierra-Sol),
(vector Tierra-Sol), 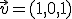 (Vector Tierra-Saturno)y
(Vector Tierra-Saturno)y 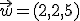 (vector Tierra-Urano). Comprueba si son una base para el espacio de tres dimensiones.
(vector Tierra-Urano). Comprueba si son una base para el espacio de tres dimensiones.
También sabe que el vector que determina la posición de Plutón (vector Tierra-plutón) es (6,6,7), pero quiere ponerlo como combinación lineal de la base anterior: 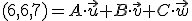
Te aconsejamos que lo resuelvas en papel primero, y después puedes comprobar si está bien utilizando el calculador azul que utilizamos en el apartado anterior.
Escribe una X en el que corresponda y una N en el que no corresponda
Los tres primeros vectores forman una base para el espacio 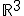 .
.
Los tres primeros vectores no forman una base para el espacio 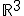
Y tenemos la combinación lineal (6,6,7)=
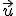 +
+
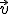 +
+
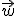
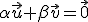 solamente puede tener una solución
solamente puede tener una solución  . Vamos a resolverla.
. Vamos a resolverla.
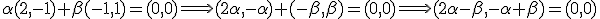
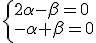
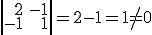
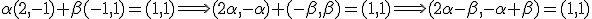

 y
y 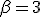 . Por tanto
. Por tanto