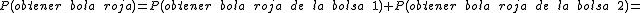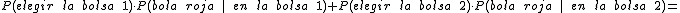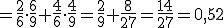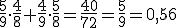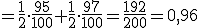2.2. La otra ley de dependencia
 |
| 1. Imagen de jlmaral bajo Licencia Creative Commons. |
En los medios de comunicación se oye constantemente hablar de la ley de dependencia para ayudar a aquellas personas que tienen a su cargo familiares con mucha edad o graves enfermedades que no les permiten valerse por sí mismas. Aquí sin embargo vamos a ver la ley fundamental que permite calcular probabilidades de sucesos que dependen de distintas situaciones. Vamos a comenzar viendo un ejemplo típico de estas situaciones.
Ejemplo o ejercicio resuelto
 |
Lanzamos un dado cúbico. Si sale 1 ó 2 extraemos una bola de una bolsa que contiene 6 bolas rojas y 3 azules. Si sale en el dado 3, 4, 5 ó 6 se extrae una bola de una bolsa que contiene 4 bolas rojas y 5 azules.
Queremos hallar la probabilidad de obtener una bola roja.
Importante
Supongamos un suceso B que depende de varios sucesos A1, A2 y A3, que tienen la característica de que abarcan todas las posibilidades de un experimento aleatorio. Para hallar la probabilidad del suceso B utilizamos la siguiente fórmula.
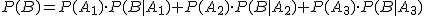
Este resultado se conoce como el Teorema de la probabilidad total. Puede ampliarse a cualquier conjunto de sucesos Ai siempre que esos sucesos sean incompatibles y juntos reúnan todos los resultados del experimento.
En el siguiente applet tomado de Matemath puedes ver ejemplos de cálculo de probabilidades a partir de la construcción de un diagrama de árbol.
En este otro tienes una página de Descartes donde te repasa el Teorema anterior y te propone una serie de ejercicios que incluimos también aquí.
Por último la siguiente escena muestra un ejercicio de ruletas, según el color que salga en la primera elegimos una ruleta distinta y queremos saber la probabilidad de obtener pares de valores. Ten presente que la suma de todas las probabilidades debe valor 1, como ya vimos en el tema anterior. Este ejercicio ha sido extraído del proyecto ed@d.
AV - Reflexión
 |
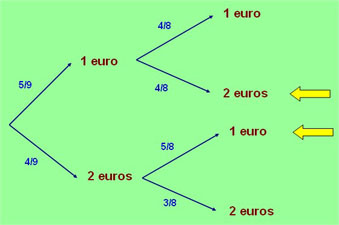
En un bolsillo tenemos 5 monedas de un euro y 4 de dos euros. Sacamos dos monedas al azar. ¿Cuál es probabilidad de que hayamos sacado en total 3 euros?
AV - Reflexión
Realiza el ejercicio de probabilidad total que te plantea la siguiente escena, exatraída del proyecto ed@d.
AV - Actividad de Espacios en Blanco
 |
En una fábrica tenemos dos cajas de tornillos, en la primera son defectuosos el 5% de los tornillos mientras que en la segunda lo son el 3%. Elegimos una de las cajas al azar y extraemos un tornillo, también aleatoriamente.
La probabilidad de que ese tornillo no sea defectuoso es de .
