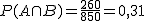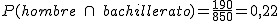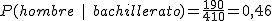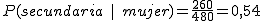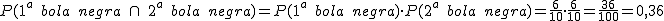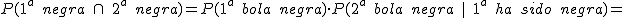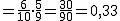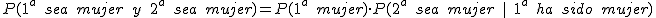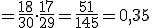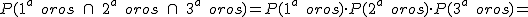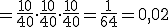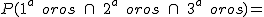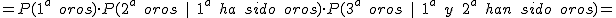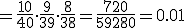2.1. La suerte también es dependiente.
 |
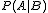 y se lee probabilidad de A condicionada a B.
y se lee probabilidad de A condicionada a B.
Posiblemente recordarás que en el tema anterior trabajamos con las tablas de contingencia y en concreto hicimos algún ejercicio con los números de matriculados en la enseñanza a distancia para adultos. Teníamos la siguiente tabla.
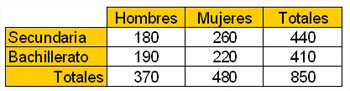 |
Si elegimos una persona al azar, de los matriculados en esta enseñanza, ¿cuál es la probabilidad de ser?
a) Alumna de secundaria.
b) Alumno de bachillerato.
c) Si la persona que hemos elegido es de bachillerato, ¿cuál es ahora la probabilidad de que sea un alumno?
d) Si hemos elegido una persona al azar y sabemos que es mujer, ¿cuál es la probabilidad de que esté matriculada en secundaria?
La probabilidad de que ocurran a la vez dos sucesos varía según sean dos sucesos dependientes o independientes. Si A y B son dos sucesos independientes la probabilidad de su intersección es:
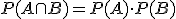
La expresión anterior se utiliza también, a veces, para definir dos sucesos independientes. Otra forma de comprobar si el suceso A es independiente de B es cuando se verifica que 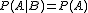 .
.
Si A y B son sucesos dependientes, entonces la probabilidad de que ocurran ambos es igual a:
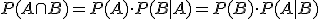
En una bolsa tenemos 10 bolas, 4 blancas y el resto negras. Extraemos primero una bola y después una segunda bola. Queremos hallar cuál es la probabilidad de que las dos bolas sean negras si:
- La primera bola se devuelve a la bolsa, tras anotar su valor.
- La primera bola se deja fuera de la bolsa antes de extraer la segunda.
En la siguiente escena, extraída del proyecto ed@d, puedes comprobar como la probabilidad cambia cuando un suceso depende de otro.
En general, si queremos hallar la probabilidad de que ocurran varios sucesos dependientes a la vez, hay que calcular la probabilidad del primer suceso, multiplicarlos por la probabilidad de que ocurra el segundo suceso, supuesto que ha ocurrido el primero, por la probabilidad de que ocurra el tercer suceso suponiendo que han ocurrido los dos primeros, y así sucesivamente. Para tres sucesos correspondería con la expresión:
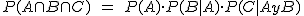
El resultado anterior se conoce como Teorema de la probabilidad compuesta y puede generalizarse a cualquier número de sucesos.
 |
Existe un grupo de personas donde hay 12 hombres y 18 mujeres. Elegimos dos personas al azar. ¿Cuál es la probabilidad de que ambas sean mujeres?
 |
Tomamos una baraja española con 40 cartas y extraemos tres cartas al azar. La probabilidad de que las tres cartas extraídas sean de oros es:
(Recuerda escribir la probabilidad con "," decimal y redondeada a dos cifras decimales)
- si las cartas se devuelven al mazo después de cada extracción.
- si las cartas que se extraen no se devuelven al mazo.