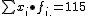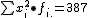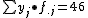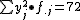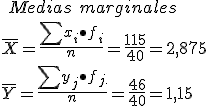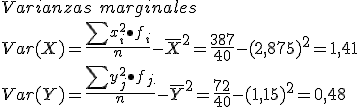4. Cada una por su lado.

Deportes

8. Deportes en 1.bp.blogpot.com bajo licencia de Creative Commons

Volviendo al ejemplo de las horas de televisión y de deporte recordemos los datos: (14, 4); (12, 6); (18, 8); (20, 6); (24, 4); (20, 2); (12, 10); (8, 8); (8, 10) ; (12, 6). Que como vimos podían representarse en una tabla bidimensional de la forma siguiente:

Horas TV (X)
 8 8 12 12 12 14 18 20 20 24
Horas deporte (Y)
 8 10 6 6 10 4 8 2 6 4

 

Ahora bien en la variable (X,Y), como ya sabes cada componente denota por sí misma una variable unidimensional con entidad estadística propia. Por tanto, si sólo recogemos los datos de las horas de TV podríamos formar la tabla:

Horas TV (X)
 8 12 14 18 20 24
fi
 2 3 1 1 2 1

 

Análogamente las horas de deporte:

Horas deporte (Y)
 2 4 6 8 10
fj
1 2 3 2 1

 

Como ya se vio en el tema anterior, como variables estadísticas unidimensionales, se pueden hallar sus medias (una de cada una), varianzas, etc.

Icono IDevice Actividad

En  una variable  bidimensional  (X, Y),  cada una de las variables por separado  (X) e  (Y )  constituyen  variables unidimensionales estadísticas. A estas  variables se les conoce como marginales:

(xi,fi)  marginal de la variable X.

(yj,fj)  marginal de la variable Y.


Icono IDevice Actividad
Recordemos el formulario


Icono de iDevice Ejemplo o ejercicio resuelto

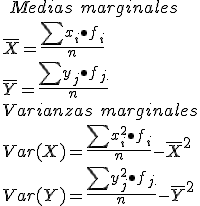
En la tabla siguiente se recogen los datos del número personas que componen la unidad familiar (X) y número vehículos por familia (Y)

X\Y 0 1 2
1 2 6 0
2 4 3 0
3 0 3 4
4
 1 8 9

 

 

1) Calcular las medias marginales

2) Varianzas marginales

3) Dibujar el diagrama de dispersión y sobre él decir qué tipo de correlación tienen estas dos variables.


Icono de IDevice de pregunta AV - Pregunta de Elección Múltiple

Sea X="nº de cambios de empleo en los últimos 5 años"

Y="nº de años en el empleo actual".

Población:Trabajadores de la empresa RISCO.

 

Tabla 35

X\Y 0 1 2 fi.
0 2 2 1
 5
1 2 3 2 7
2 2 1 2 5
3
 1 1 1 3
f.j 7 7 6 n=20

Según estos datos

1.- El número medio de cambios de empleo de la empresa es (media de X)

  
a) 2,5
b) 1,5
c) 1,3

2.- La antigüedad media de los trabajadores en la empresa es de:
  
a) 0,95 años
b) 1,95 años
c) 1,6 años

3.- las varianzas de X e Y respectivamente son:
  
a) (1,01; 0,65)
b) (0,65; 1,01)
c) (1; 0,9)

« Anterior