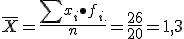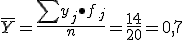2. Las tablas dobles.
|
|
5. Imagen de reglasdecalculo bajo licencia Creative Commons |
La representación más utilizada para una variable estadística bidimensional es de una tabla.
Los datos aparecen emparejados, agrupados o no.
En el ejemplo del apartado anterior podíamos expresarlos con la siguiente tabla:
| Horas TV | Horas Deporte |
| 14 | 4 |
| 12 | 6 |
| 18 | 8 |
| 20 | 6 |
| 24 | 4 |
| 20 | 2 |
| 12 | 10 |
| 8 | 8 |
| 8 | 10 |
| 12 | 6 |
Para ser más operativos es recomendable ordenar los datos de menor a mayor respecto a una de las variables (lógicamente la otra no tiene que estar ordenada por regla general)
Si lo hacemos respecto a las horas de televisión la tabla quedaría:
| Horas TV (X) |
8 | 8 | 12 | 12 | 12 | 14 | 18 | 20 | 20 | 24 |
| Horas deporte (Y) |
8 | 10 | 6 | 6 | 10 | 4 | 8 | 2 | 6 | 4 |
Nos preguntamos si en vez de diez datos recogemos 100, 1000 o más ¿cómo sería de larga esta tabla?
Para ello existen las tablas de doble entrada, que es la otra forma de expresar los datos (datos agrupados).
El ejemplo siguiente recoge los datos de una variable bidimensional (X, Y) donde
X=" nº de varones"
Y="nº de mujeres"
Tabla 32
| X\Y | 0 | 1 | 2 |
| 0 | 2 | 1 | 2 |
| 1 | 4 | 3 | 0 |
| 2 | 2 | 2 | 1 |
| 3 |
1 | 2 | 0 |
¿Cómo interpretar una tabla de este tipo?
La primera columna denota el número de varones (X), la primera fila (Y), el número de mujeres.
Sin contar la fila y columna de las variables, la tabla de 4 filas y 3 columnas (en blanco) es la tabla de frecuencias absolutas que denotaremos por fij siendo i=n.º de fila y j=n.º columna, de forma que, por ejemplo, f21=4 denota el número de familias con un varón y no tienen niñas, f43=0 significa que no hay ninguna familia con 3 varones y 2 niñas.
Aprendamos un poco de notación
(ver tabla 33)
. Tamaño de la muestra "n" (en naranja) 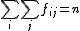 . Sumaremos las columnas y los resultados los sumaremos como una fila o bien sumamos todas las frecuencias absolutas fij.
. Sumaremos las columnas y los resultados los sumaremos como una fila o bien sumamos todas las frecuencias absolutas fij.
. Distribución marginal de la X (en celeste), 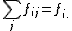 . Sumando las filas obtendríamos la tabla unidimensional del número de varones.
. Sumando las filas obtendríamos la tabla unidimensional del número de varones.
. Distribución marginal de la Y (en lila) , 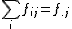 . Sumando las columnas obtendríamos la tabla unidimensional del número de mujeres.
. Sumando las columnas obtendríamos la tabla unidimensional del número de mujeres.
. Media marginal de la variable X: 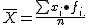
. Media marginal de la Y: 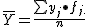
![]()
Tabla 33
| X\Y | 0 | 1 | 2 | fi. |
| 0 | 2 | 1 | 2 | 5 |
| 1 | 4 | 3 | 0 | 7 |
| 2 | 2 | 2 | 1 | 5 |
| 3 |
1 | 2 | 0 | 3 |
| f.j | 9 | 8 | 3 | n=20 |
 |
|
6. Niñas o niños. Imagen de elbuendiario bajo licencia Creative Commons |
Según los datos que aparecen en la tabla 32.
1.- ¿Cuántos matrimonios hemos encuestado?
2.- ¿Cuántas familias sólo tienen varones?
3.- ¿De las familias con un varón que porcentaje tienen 1 mujer?
4.- ¿Qué media de varones tienen estas familias?
5.- ¿Cuál es la media de hijas?
En la tabla 35 X="n.º de cambios de empleo en los últimos 5 años" e Y="n.º de años en el empleo actual". Población:Trabajadores de la empresa RISCO.
Tabla 35
| X\Y | 0 | 1 | 2 | fi. |
| 0 | 2 | 2 | 1 |
5 |
| 1 | 2 | 3 | 2 | 7 |
| 2 | 2 | 1 | 2 | 5 |
| 3 |
1 | 1 | 1 | 3 |
| f.j | 7 | 7 | 6 | n=20 |
Según estos datos
1.- ¿ Cuántos trabajadores no han cambiado de empleo en los últimos 5 años?
|
a) 5
| |
|
b) 7
| |
|
c) 20
|
|
a) 6
| |
|
b) 1
| |
|
c) 3
|
|
a) El 50%
| |
|
b) 10
| |
|
c) 12
|