3.1. El exponente crece
 |
| Imagen de kryfil.com bajo licencia Creative Commons |
Ya sabes que Juan es bastante conocedor de las matemáticas y sabe que la figura rectangular que tiene mínimo perímetro con un área fijada es el cuadrado. Es decir, que si queremos que una figura rectangular tenga una determinada superficie y queremos que el material para su construcción sea mínimo, debemos construirlo de forma cuadrada.
Pues bien; Juan desea poner un mostrador expositor con una serie de artículos de complemento que ocupe el centro de su nueva tienda del centro comercial, y según las estimaciones que ha hecho, debe tener una superficie de 6 metros cuadrados, entonces, ¿qué longitud debe tener el expositor?
Si llamamos x a la longitud del lado del cuadrado y puesto que el área de un cuadrado es lado por lado, tendremos que tiene que cumplirse que:
x·x = 6, o lo que es lo mismo, x2 = 6.
Este es un ejemplo de ecuación de segundo grado; una ecuación donde x aparece elevada al cuadrado.
Actividad
Una ecuación de segundo grado es una ecuación que tras simplificarla y pasar todos los términos a un lado queda de la forma:
ax2 + bx + c = 0.
Para resolverlas se usa la fórmula:
Ejemplo o ejercicio resuelto
AV - Reflexión
 |
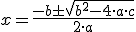
| Imagen de J.P.Esperança bajo licencia Creative Commons. |
En la siguiente escena vas a resolver ecuaciones de segundo grado.Pulsa sobre el botón ejercicio. Resuelve la ecuación que aparece y antes de introducir los valores, en las casillas para comprobar, elige la opción que se ajuste a tu caso en la ventana "Tipo de solución". Seleccionada esta introduce los valores de las soluciones y pulsa sobre el botón "solución" para comprobar si lo has hecho bien.
Applet Descartes de Miguel Ángel Cabezón Ochoa bajo licencia Creative Commons.
Objetivos
En la animación puedes ver de dónde sale esa fórmula:
|
|
| Animación publicada en Descarte/EDAD bajo licencia Creative Commons |
Actividad
Como puedes ver, a veces hay dos soluciones, a veces una y otras no tienen solución.
Esto depende del número que nos quede dentro de la raíz, o sea, del valor de la expresión
"b2 - 4·a·c",
que se llama discriminante:
- Si es positivo, hay dos soluciones.
- Si es cero, hay una única solución.
- Si es negativo, no existe solución, pues como sabes, la raíz cuadrada de un número negativo no existe.
AV - Reflexión
En la siguiente actividad con Jclic, puedes practicar esto último.
Applet Java modificado del original de Juan José Menéndez Díaz publicado en zonaClic bajo licencia Creative Commons
Pre-conocimiento
Fíjate cómo resolvía estas ecuaciones Al- Jwuarizmi.
|
|
| Animación publicada en Descarte/EDAD bajo licencia Creative Commons |
Objetivos
Otro tipo de ecuaciones con grado mayor que 1 son las llamadas ecuaciones bicuadradas. Estas ecuaciones son de la forma:
ax4 +bx2 + c = 0.
Se resuelven reduciéndolas a ecuaciones de segundo grado y aplicando todo lo que hemos visto en el apartado.
Puedes verlos y practicar siguiendo el enlace.