2.4. Pagando todos los meses
En todos los ejemplos que hemos hecho sobre operaciones de capitalización hemos supuesto que las aportaciones se hacían anualmente (anualidades). No obstante, esto no tiene que ser necesariamente así. Los pagos pueden hacerse mensualmente, trimestralmente, semestralmente,... Veamos unos ejemplos para aprender a adaptarnos a estas situaciones.
Ejemplo 1.: (Haz clic sobre la presentación para avanzar)
Antes de seguir, con esta materia un tanto complicada, un poco de humor:
Ejemplo 2: (haz clic sobre la presentación para avanzar)
 Pregunta de Elección Múltiple
Pregunta de Elección Múltiple
Contesta las dos cuestiones:
Mariano ingresa 3.000 euros semestralmente en un fondo. La entidad financiera le da un 4 % de interés. ¿Qué capital tendrá al cabo de 5 años?
Piensa en la fórmula que debes utilizar, cuántos pagos se hacen y como afectan este fraccionamiento del año al interés.
Esa es la cantidad aportada por Mariano, le faltan los intereses.
Has utilizado la fórmula de las anualidades, como si se hiciese un pago cada año. Observa que dice pagos semestrales.
Fenomenal. 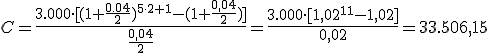 €.
€.
Revisa las operaciones y/o los contenidos.
Una familia desea disponer de 80.000 € dentro de 10 años. Han encontrado un banco que le ofrece un interés del 6% anual haciendo aportaciones bimestrales. ¿De cuánto debe ser cada pago bimestral?.
Piensa qué quieres hallar, cuál es la fórmula apropiada y cómo afecta el que se hagan pagos bimestrales.
Muy bien.
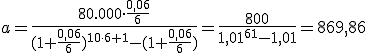
€.
Cuidado, no has tenido en cuenta los intereses y has repartido el total entre los 60 pagos.
Cuidado, es posible que no hayas tenido en cuenta que los pagos son bimestrales.
Puede que tengas mal las operaciones o que hayas interpretado mal el problema.
 Objetivos
Objetivos
Es posible también, sabiendo la cantidad que queremos aportar en cada período, el capital que se desea obtener al final y el interés anual, determinar el número de períodos necesarios, es decir, el tiempo que debemos estar pagando.
Veámoslo en un ejemplo: ¿Cuántos años debe estar Manuel aportando dinero a un fondo si piensa hacer aportaciones anuales de 4.000 euros a un interés anual del 3% y quiere obtener un capital final de 50.000 euros?
Bueno, con fórmula
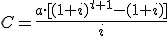 , tenemos:
, tenemos: 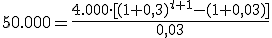
=> 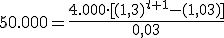 ,
,
y despejando,
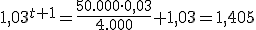
y tomando logaritmos:
=>
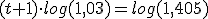
de donde: 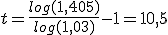 años.
años.
Habrás observado que necesitamos del uso de logaritmos, si no recuerdas esta operación, puedes recurrir al enlace que te ponemos de la wikipedia.
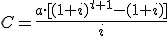 , tenemos:
, tenemos: 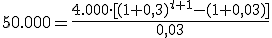
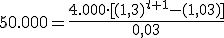 ,
,
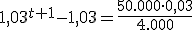
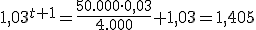
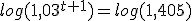
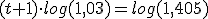
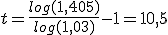 años.
años.

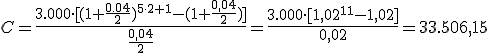 €.
€.
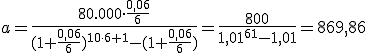 €.
€.