2.2. Interés compuesto
 |
| 17. Imagen de itson bajo licencia Creative Commons |
Ya hemos visto cómo se calcula el interés (beneficio) que un capital produce en un año.
En realidad, don Ramón pensó que si en un año no retira sus intereses ¿que pasa con el dinero que produce esos intereses?
Cuando los intereses producidos por un capital se van acumulando al capital para producir nuevos intereses, el interés se llama compuesto:
Las fórmulas para el tiempo en años, meses y días son las siguientes, en las que t representa el número de años, meses o días que se va a tener invertido el dinero:
Caso de estudio
Capital inicial c=60.000 t= 1 año r=8% Apliquemos la fórmula:
En el primer año obtendría 4800, veamos el 2º:
En la tabla de abajo observarás la diferencia en tres años del capital producido al mismo tanto por ciento con el interés simple y el compuesto.
| Interés Simple | Interés Compuesto | Diferencia |
| 64.800 |
64.800,00 |
0 |
| 64.800 | 69.984,00 |
5.184,00 |
| 64.800 | 75.582,72 |
10782,72 |
Caso de estudio
 |
| 18. Imagen de jerezsiempre bajo licencia Creative Commons |
Con un capital inicial de 30.000 € a un 4,5%, ¿con qué capital nos encontraremos? a) 5 años b) 125 meses c) 2.200 días.
a) Aplicamos la fórmula para el interés compuesto para años.
c) Para días:
Pre-conocimiento
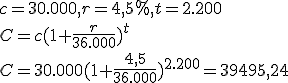
Bien, ha llegado el momento de comprobar que el viejo de la historia inicial tenía razón y todas las de ganar en su pelea con Marina.
Recordamos que invirtió 23,72€ al 7,8% durante 10 años.
Aplicando la fórmula, el capital que debe obtener al final es:
que es 50,269236... y redondeado a los céntimos 50,27
AV - Reflexión
La siguiente escena te permite practicar con los ejercicios de interés compuesto o capitalización compuesta como los llama.
Applet de Miguel Ángel Martín bajo licencia Creative Commons
Pre-conocimiento
Algunos vídeos curiosos en los que se aplica el interés compuesto en la vida cotidiana:
|
|
|
|
|
|
|
|
|