3. Llegamos a un punto de inflexión.
| Cóncavo |
Cóncavo (abajo) y Convexo (arriba) |
Convexo |
 |
 |
 |
|
Puente de la Barqueta, de Tutty,
|
Concave, de MS-R,
|
DSC02280b, de jackace,
|
Mira las curvas de las fotos. Otra de las características de las funciones es su curvatura, y los objetos que aparecen en las imágenes de arriba tienen diferente curvatura.
Si coges dos puntos de la parte superior del puente y los unes con una cuerda, ésta quedará por debajo de la curva (es cóncavo). En el caso de la rampa, si unimos dos puntos la cuerda queda por encima (es convexa).
La curvatura de una función también se puede estudiar a partir de las derivadas. En la siguiente escena de geogebra, mueve el punto P a lo largo de la función para ver cómo varía la monotonía y la curvatura de la función.
Observa el cambio en la primera y segunda derivada en los puntos de abscisa x=-1, x=0, x=1, x=2 y x=3, e intenta averiguar la relación. Pulsando las casillas de monotonía y curvatura verás los intervalos en los que cambian estas dos características.
Importante
En una función dos veces derivable, podemos estudiar la curvatura de la siguiente forma:
- Convexa (U): será convexa en los intervalos donde f ''(x) > 0.
- Cóncava (∩): será cóncava en los intervalos en los que f ''(x) < 0.
- Puntos de inflexión: son los puntos donde cambia la curvatura. Por tanto se cumple que f ''(x)=0.
Y ahora, como hemos hecho en los apartados anteriores, veremos un ejercicio resuelto.
¿Te atreves a estudiar la curvatura de una función? Aquí tienes un problema sencillo.
AV - Actividad de Espacios en Blanco
Necesitamos estudiar la curvatura de la función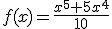
para un proyecto que estamos realizando. Completa los campos en blanco con los resultados que obtengas:
- La primera derivada de la función es f '(x) = (x4+ x3) /
- La segunda derivada es f ''(x) = x3+ x2
- La función f(x) es cóncava en (-∞, )
- La función f(x) es convexa en ( ,+∞)
- Tiene un punto de inflexión en P=( , )
- ¿Existe punto de inflexión en x=-3? (sí/no)
Ejemplo o ejercicio resuelto
¡Cuidado con los picos! Todo lo que hemos visto funciona perfectamente si estamos trabajando con funciones continuas y derivables, pero por desgracia no siempre podemos contar con que nuestra función tenga esas condiciones... Por ejemplo, observa la siguiente gráfica:
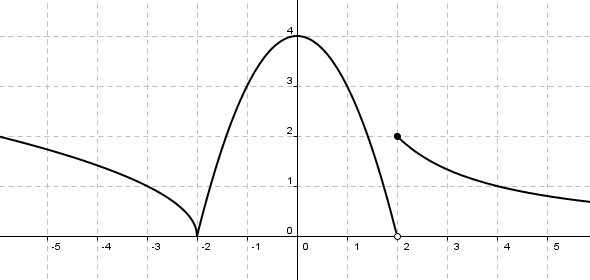
Por la gráfica, ¿cuáles son sus máximos y mínimos absolutos y relativos? (La parte de la izquierda no tiene ningúna asíntotal horizontal, y por tanto no se estabiliza alrededor de ningún valor.)
La función que tenemos representada es:
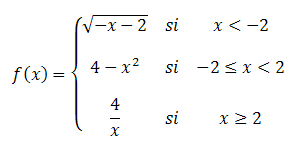
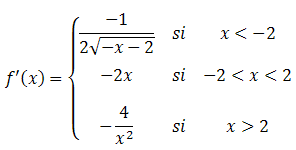
Esta función es continua en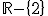 
y derivable en 
.
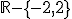Sabemos que los máximos y los mínimos cumplen que f '(x) = 0, pero en x=-2 no existe derivada, y sin embargo tenemos un mínimo. Igualmente nos ocurre en x=2. Si igualamos a cero la derivada, en sus tres trozos, sólo obtendremos un punto posible: x=0 ¿Qué ocurre entonces?
Para estudiar los máximos y mínimos de una función que no es derivable, hay que estudiar:
- Los puntos en los que se anula la primera derivada en la parte que sea una función derivable.
- Los puntos donde la función no es derivable.
Nos ocurrirá lo mismo para los puntos de inflexión.
Estudia el crecimiento y decrecimiento con la primera derivada en cada uno de los trozos de la función.