4. Funciones populares

Al igual que en Literatura nos encontramos con obras clásicas como la "Ilíada" de Homero, en música las "Sinfonías" de Beethoven, o en el cine con películas como "2001, una odisea en el espacio" de Kubrick. En el mundo de las relaciones funcionales, ese papel de clásicas lo interpretarías las funciones afines y cuadráticas.

Importante

Las funciones polinómicas de primer grado, también llamadas funciones afines son aquellas cuya ecuación es del tipo f(x) = mx + n

Algunas de sus características principales son:

Su dominio es todo	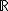Si m > 0, la función es creciente
Su gráfica es una recta con pendiente m	Si m < 0, la función es decreciente
Pasa por el punto (0,n) [Punto de corte con el eje OY]

Dentro de las funciones afines podemos distinguir dos tipos. En una función afín: f(x) = mx + n

· Si m = 0, la función y = n se denomina función constante. Su gráfica es una recta paralela al eje OX, que pasa por el punto (0,n)

· Si n = 0, la función y = mx se denomina función lineal y su gráfica es una recta de pendiente m que pasa por el origen de coordenadas (0,0)

Comprueba y practica las características de las funciones afines con el siguiente applet de Wiris. Simplemente deberás seleccionar los valores para m (pendiente) y n (ordenada en el origen).

AV - Actividad de Espacios en Blanco

Imagen de isaleal con licencia CC BY 2.0

Con motivo de la celebración de la semana cultural en una gran ciudad, se ha considerado poner una tarifa plana en el precio de las entradas para acudir a las distintas representaciones teatrales que se celebran esa semana. Se ha establecido una tarifa de 12 euros por persona.

(a) Obtén la ecuación de la función que nos permitirá calcular la recaudación obtenida en cada teatro, en función del número de asistentes.

(b) Si en un determinado teatro se ha completado el aforo para asistir a una obra y se ha recaudado un total de 8400 €. ¿Cuál es el aforo, la capacidad, del teatro? Es decir, ¿cuántas entradas se han vendido?

Resolvamos el problema.

(a) La función es f(x) = JXUwMDY5JXUwMDAzJXUwMDRh donde x es el número de asistentes.

(b) El aforo máximo del teatro es de JXUwMDZmJXUwMDA3JXUwMDAw personas.

Ejemplo o ejercicio resuelto

Imagen de M. Peinado con licencia CC BY 2.0

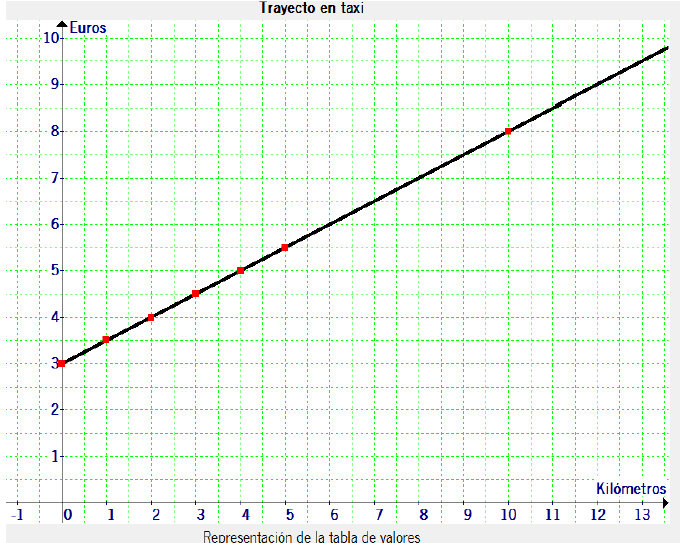
El precio del trayecto de un taxi tiene un coste fijo de 3 €, más 0,5 € por cada
kilómetro recorrido. Para asistir a la obra de teatro, cogemos uno.

(a) Elabora una tabla de valores de la función
(kilómetros - euros) de nuestro taxi y realiza una representación
gráfica a partir de dicha tabla.

(b) Halla la ecuación de dicha función y calcula su
pendiente.

Nota: Puedes realizar la representación gráfica con Geogebra, apoyándote en el procedimiento que describe en esta construcción.

Vayamos por partes.

· Datos:
Coste fijo por trayecto por valor de 3 €
0,5 € por cada Kilómetro recorrido.

· Planteamiento:
Tras leer el enunciado del problema observamos que: El coste del trayecto es la suma de una parte fija más una variable.
El coste del trayecto (y) se obtendrá como suma de estos dos factores. El fijo (3 euros) y el variable, que será proporcional, con un factor constante de 0,5, al número de kilómetros del trayecto (x)

· Resolución:

(a) Tabla de valores:
Supondremos trayectos con valores naturales, exactos, para los kilómetros, con el único fin de simplificar la elaboración de la gráfica que debemos realizar posteriormente.

Kilómetros (x)	0	1	2	3	4	5	10
Euros (y)	3	3,5	4	4,5	5	5,5	8

Representación gráfica.

(b) Ecuación de la función que calcula el coste del trayecto.

Tal y como indicado en el planteamiento, el coste de un trayecto viene dado por la suma de 2 partes: una fija y otra proporcional al número de kilómetros recorridos.

Así, la ecuación vendrá dada por:

{Coste del trayecto=Coste fijo + Coste proporcional a km recorridos}
y= f(x) = 3 + 0,5⋅x

Observamos que hemos obtenido una función afín. Por tanto, es posible deducir la pendiente de su propia expresión, ya que como sabemos, una función afín viene dada por: y = m·x + n, donde m es la pendiente de la función y n, el valor de la ordenada en el
origen.

Así, igualando, y = m·x + n con y = 0,5·x + 3, obtendremos que la pendiente = m = 0,5.

(c) Distancia en metros del trayecto.
Nos han cobrado 6,25 € por un trayecto. Para averiguar la distancia que hemos recorrido, basta hacer y = 6,25 en la ecuación de la función y obtener x.
y = 0,5·x + 3 → 6,25 = 0,5·x + 3 → 6,25 – 3 = 0,5·x → 3,25 = 0,5·x → x = 3,25 / 0,5 → x = 6,5 kilómetros.
Como nos piden el trayecto en metros, basta convertir, de kilómetros a metros, multiplicando por 1000.

Así, la distancia, en metros, del trayecto es de 6500 metros.

Imagen de tegioz con licencia CC BY 2.0

Desarrollamos a continuación el estudio de otra de las familias con historia en el mundo de las funciones. Nos referimos a las ya mencionadas funciones cuadráticas.

Actividad

Las funciones polinómicas de segundo grado, también llamadas funciones cuadráticas son aquellas cuya ecuación es del tipo:

f(x) = ax² + bx + c, con .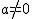

Algunas de sus características principales son:

Su dominio es todo	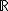El vértice de la parábola es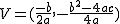
Su gráfica es una parábola, simétrica respecto a eje de simetría que pasa por su vértice.	Cuanto mayor sea el valor absoluto de a, \|a\|, más cerrada será la parábola.
Si a > 0 el vértice de es un mínimo absoluto	Si a < 0 el vértice es un máximo absoluto
Si a > 0 es una función convexa	Si a < 0 es una función cóncava

Entre las funciones cuadráticas podemos distinguir tres tipos especiales, que se corresponden con otras tantas ecuaciones incompletas.

En una función cuadrática f(x) = ax² + bx + c, con .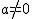

· Si b = 0 y c = 0, la función f(x) = ax² tiene su vértice en el punto (0,0) y su eje de simetría es el eje OY

· Si b = 0 y 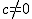, la función f(x) = ax² + c tiene su vértice en el punto (0,c) y su eje de simetría es el eje OY

· Si 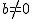y c = 0, la función f(x) = ax² + bx tiene su vértice en el punto 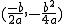y su eje de simetría es la recta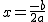

Comprueba y practica las características de las funciones cuadráticas con el siguiente applet de Geogebra. Simplemente deberás desplazar los deslizadores para configurar los valores de los coeficientes a, b y c.

Ejemplo o ejercicio resuelto

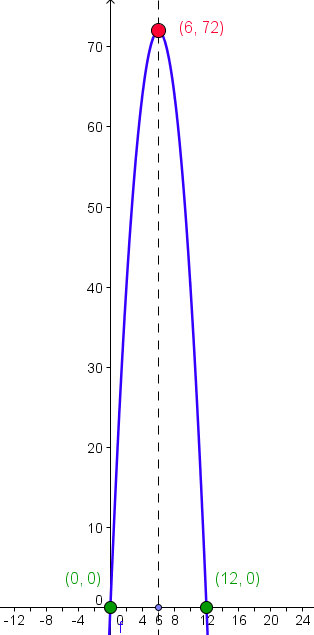
Al rojo vivo.

La función T(t) = 24t - 2t², con 0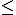t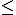12 , devuelve la temperatura, T, en grados centígrados, que alcanza el motor de una máquina de fabricación industrial en función del tiempo, t, en horas, que lleve funcionando.

(a) Realiza la tabla de valores y representa la gráfica de la función.

(b) ¿Qué temperatura alcanza el motor al cabo de 2 horas de funcionamiento?

(d) Observa la gráfica y describe: el dominio, recorrido, la monotonía y la simetría (par/impar) de la función.

Nota: Puedes realizar la representación gráfica con Geogebra, apoyándote en el procedimiento que describe Jesús Fernández en esta presentación. A la hora de representarla deberás usar la variable "x" en vez de la variable "t".

Como siempre, vayamos por partes.

· Datos

La función T(t) = 24t - 2t² , con 0t12 que devuelve la temperatura que alcanza el motor de la máquina en función del tiempo que lleve funcionando la misma.

· Planteamiento:

Tras leer el enunciado del problema observamos que: la ecuación de la función es de segundo grado y por tanto, su representación gráfica
será una parábola.

A fin de facilitar la representación de la misma al estudiante, se le pide elaborar tabla de valores para posteriormente representarla.

En primer lugar haremos la tabla, posteriormente la representaremos y, finalmente, responderemos a las cuestiones, del resto de apartados, interpretando la gráfica.

· Resolución:

(a)

Tabla de valores:

Tiempo en horas (t)	0	1	2	3	4	5	6	7	8	9	10	11	12
Temperatura en ºC	0	22	40	54	64	70	72	70	64	54	40	22	0

Representación gráfica.

(b) Basta observar la gráfica para comprobar que, a las t=2 horas de funcionamiento la temperatura es T(2)=40 ºC.
También se puede encontrar este valor, buscando en la tabla de valores.

(c) El motor alcanza su temperátura máxima en el vértice de la parábola, esto es, para t=6. A las 6 horas de funcionamiento alcanza su temperatura máxima.

El valor de la temperatura máxima es T(6)=72 ºC, basta observar la gráfica o buscarlo en la tabla de valores.

(d)

- Dominio: [0,12] Tiempo en horas que está en funcionamiento. Sólo funciona 12 h
- Recorrido: (0,72) Temperatura que alcanza el motor en funcionamiento. Rango de temperaturas que alcanza el motor.
- Monotonía: Crece en el intervalo (0,6). Decrece en (6,12). La temperatura va aumentando hasta que alcanza el máximo en el vértice de la parábola, a las 6 horas de funcionamiento. A partir de ahí, decrece hasta alcanzar los 0 grados a las 12 horas.
- Simetría: La gráfica es simétrica respecto de la recta: x=6, que pasa por el vértice de la parábola y es perpendicular al eje OX. No es ni PAR ni IMPAR.

Objetivos

Si quieres consolidar y ampliar tus conocimientos sobre el tema, puedes hacerlo en esta unidad del Proyecto Descartes realizada por Josep Mª Navarro Canut.

Tablas y expresiones algebraicas

« Anterior