3. Transformaciones. Cambios en el decorado
Ya han transcurrido dos actos y seguro que habrás observado que el decorado ha cambiado entre uno y otro. Cae el telón al finalizar un acto y, cuando vuelve a levantarse, ¡sorpresa! Al levantarse de nuevo vemos que el decorado del escenario ha cambiado completamente o que se transformado, algunos objetos han desaparecido y otros han cambiado de ubicación. Han sido desplazados. Más hacia la derech o izquierda, más hacia arriba o abajo. Tal vez, una mezcla de ambas situaciones.
Las funciones también pueden sufrir transformaciones. Desplazamientos en horizontal en vertical, e incluso cambios de forma.
Del análisis de estas transformaciones nos encargaremos a continuación.
 |
| Imagen de kevindooley con licencia CC BY 2.0 |
Trasladar una función, y = f(x), verticalmente k unidades consiste en sumarle a la variable dependiente (y) la constante (k).
Obtenemos así una nueva función: y = f(x) + k
· Si k es positiva, entonces, la función se traslada hacia arriba.
· Si k es negativa, entonces, la función se traslada hacia abajo.
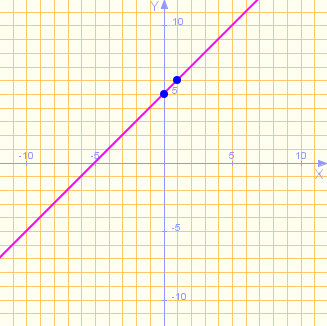
Completa los espacios en blanco relacionados con traslaciones verticales de las funciones afines representadas a continuación:
 |
 |
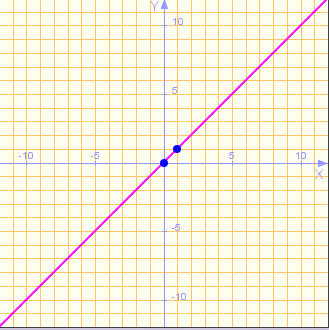 |
| Gráfica Nº 1 | Gráfica Nº 2 |
Gráfica Nº 3 |
(a) La gráfica de la función f(x) = x es la Gráfica Nº
(b) Al, desplazar, aplicar una traslación vertical del tipo y = f(x) + 5 a la Gráfica Nº 1 obtendremos la Gráfica Nº
(c) La gráfica de la función f(x) = x - 5 es la Gráfica Nº
(d) Al, desplazar, aplicar una traslación vertical del tipo y = f(x) - 5 a la Gráfica Nº 3 obtendremos la Gráfica Nº
(e) La gráfica de la función f(x) = x + 5 es la Gráfica Nº
 |
| Imagen de Nikki Graziano |
Found Functions.
¿Te gustaría ver gráficas de funciones describiendo y adaptándose perfectamente a la naturaleza, como la que aparece a la izquierda?
Accede a la exposición virtual de Nikki Graziano y disfruta de esta maravilla de trabajo.
Trasladar una función, y = f(x), horizontalmente, p unidades consiste en restarle a la variable independiente (x) la constante (p).
Obtenemos así una nueva función: y = f(x-p)
· Si p es positiva, entonces, la función se traslada hacia la derecha.
· Si p es negativa, entonces, la función se traslada hacia la izquierda.
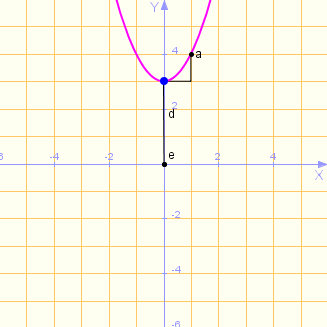
Ayúdate del applet de Wiris anterior y de la definición de traslaciones vertical, horizontal y oblicua para completar los espacios en blanco siguientes relacionados con las imágenes adjuntas:
 |
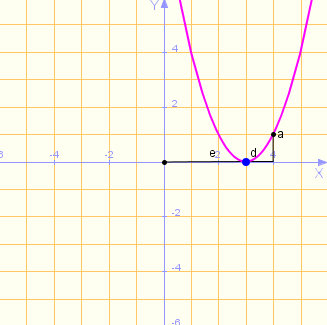 |
| Gráfica Nº 1 | Gráfica Nº 2 |
 |
 |
| Gráfica Nº3 | Gráfica Nº 4 |
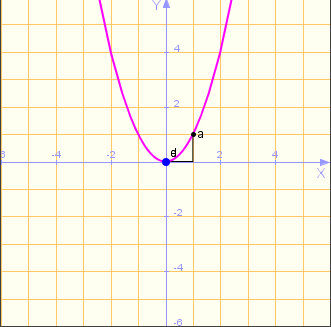
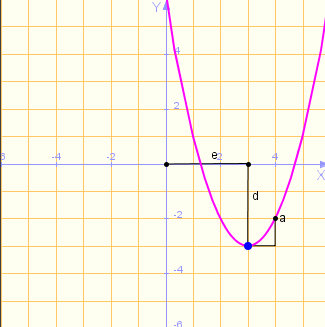
(a) La gráfica de la función f(x) = x2 es la Gráfica Nº
(b) Si aplicamos una traslación horizontal de p=3 unidades, es decir, del tipo y = f(x-3) a la Gráfica Nº 3, obtendremos la Gráfica Nº
(c) La gráfica de la función f(x) = x2 + 3 es la Gráfica Nº
(d) Si aplicamos una traslación horizontal de p=3 unidades, más una traslación vertical de k=-3 unidades, es decir, una transformación oblicua y = f(x-3) - 3 a la Gráfica Nº 3, obtendremos la Gráfica Nº
 |
|
Calculus. Fuente: Djerassi.com
|
En la obra de teatro titulada Calculus y escrita por Carl Djerassi se relata el nacimiento del cálculo infinitesimal y la polémica que mantuvieron sus dos creadores: el inglés Sir Isaac Newton y el alemán Gottfried Wilhelm Leibniz.
Para saber más, consulta:
Divulgamat. Teatro y Matemáticas y la página del propio autor de la obra de teatro, otro científico sobresaliente: Carl Djerassi, químico, novelista y dramaturgo, conocido por su contribución en el desarrollo de la píldora anticonceptiva.
Del mismo modo que las funciones pueden cambiar de lugar, trasladarse, también pueden cambiar de forma, mediante lo que se denominan contracciones o dilataciones.
· Una función, f(x), se contrae si realizamos la siguiente operación: f(k·x) con k > 1
· Una función, f(x), se dilata si realizamos la siguiente operación: f(k·x) con 0 < k < 1
 |
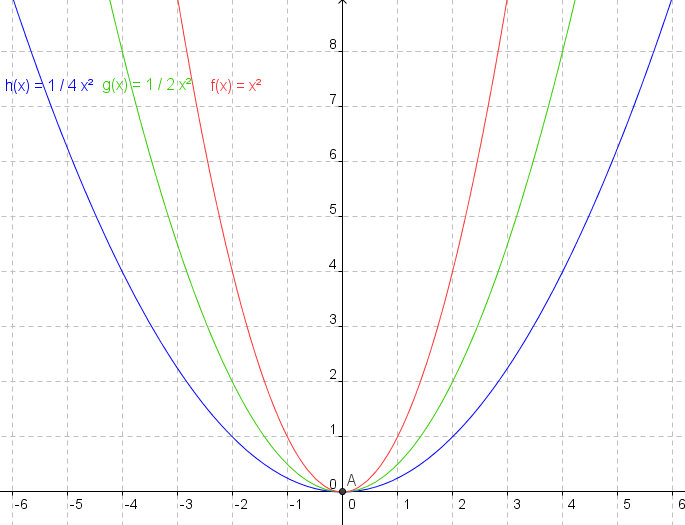 |
| Contracciones | Dilataciones |