2.2. Del dominio al recorrido
La variable independiente x, del ejemplo anterior, varía en el intervalo [0, 5], es decir, el agua de la piscina puede estar entre los 0 y 5 metros. A este intervalo se le llama dominio de la función f.
Por otro lado, la variable independiente y, varía en el intervalo [0, 1250], lo que significa que los metros cúbicos que tiene la piscina se mueven entre los 0 y 1250. A este otro intervalo se le denomina recorrido de la función.
Actividad
Llamaremos dominio de una función f al conjunto de valores que toma la variable independiente, x. Lo denominaremos D(f).
En tanto que, llamaremos recorrido de f al conjunto de valores que toma la variable dependiente, y. Lo denotaremos R(f).
En el ejemplo de la piscina 2, D(f)=[0, 5] y R(f)=[0,125].
AV - Actividad de Espacios en Blanco
Objetivos
En el siguiente enlace que corresponde a una unidad didáctica del proyecto Edad del Ministerio de Educación, puedes practicar el cálculo de dominios y recorridos.
AV - Actividad de Espacios en Blanco
 |
Para terminar, vamos a volver a la empresa de tratamiento de aguas.
La piscina 3, tiene la forma que aparece en la imagen. Como puedes ver es escalonada. Mide 5 metros de profundidad, 10 de ancho y 50 de largo, como las otras. En la escena de GeoGebra se aprecia el perfil de la piscina. Como en las otras ocasiones, haciendo clic en el control puedes comprobar cómo se va llenando y la relación que hay entre la altura del agua y los metros cúbicos que contiene.
Rellena los siguientes espacios en blanco.
a) La relación es una función, puesto que a cada altura en metros, le correspode una cantidad de metros cúbicos de agua.
b) f(1) = .
c) f(
) = 750.
d) El recorrido de la función es el intervalo [ , ].
Para saber más
A lo largo de toda esta unidad, y en unidades anteriores, hemos utilizado escenas de GeoGebra que nos han servido para manipular algunos de los conceptos que se trabajaban en cada momento.
GeoGebra es una magnífica herramienta que nos permite representar funciones conocidas su expresiones algebraicas. En la siguiente presentación se explica de forma breve cómo hacerlo.
AV - Actividad de Espacios en Blanco
Asocia a cada una de las siguientes funciones que vienen dadas por su expresión analítica, su dominio.
 |
 |
 |
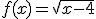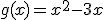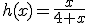a) El dominio de (x) son todos los números reales, es decir R.
b) La función (x) tiene como dominio todos los números reales menos el -4. Esto lo podemos expresar como R-{-4}
c) Todos los números mayores o iguales que 4, es decir el intervalo [4, +∞) es el dominio de la función (x).
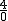, y no es posible dividir entre 0.