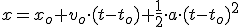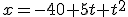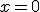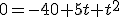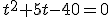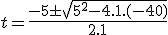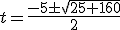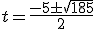2.2 Ecuación posición-tiempo de un MRUA
Ahora vamos a intentar obtener una ecuación para la posición parecida a la que hemos deducido para la velocidad. Seguimos trabajando sobre el ejemplo anterior.

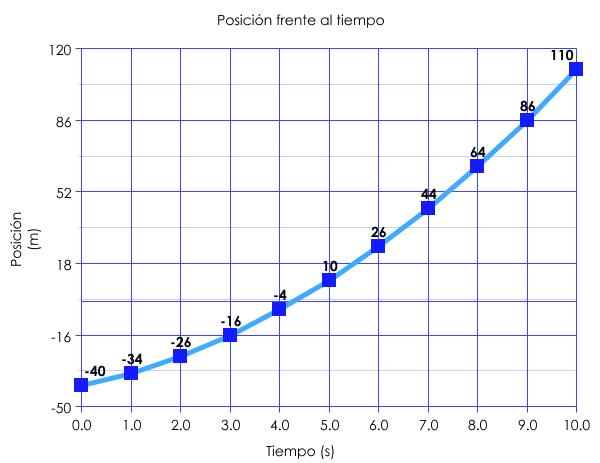
Esta gráfica ya no es una recta como ocurría en el caso de un MRU. Sin embargo es una curva muy conocida en Matemáticas. Se trata de una parábola. ¿Recuerdas su ecuación?
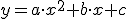
Claro en matemáticas se usan la "x" y la "y" como variables independiente y dependiente pero en nuestro caso la variable posición (x) depende de la variable tiempo(t) por lo que en Física solemos escribir la ecuación espacio-tiempo de este modo:
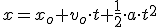
¿Qué significan los términos que aparecen en esta ecuación? Pues xo es la posición del móvil en el instante inicial (-40 m), vo la velocidad inicial (5 m/s) y a la acelaración (2m/s2). La anterior ecuación general en el caso de nuestro caso concreto quedaría así:
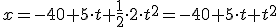
Teniendo esta ecuación ya no solo conozco la posición en los tiempos que aparecen en la tabla sino en cualquier otro instante. Por ejemplo podría calcular en qué posición se encuentra el móvil a los 3,5 segundos. Para ello basta con sustituir la t por 3,5.
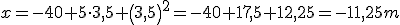
Cuando estemos midiendo el tiempo antes de que comience el movimiento de nuestro objeto a estudio, la ecuación anterior no nos servirá. Con una pequeña modificación tenemos la ecuación que describe la posición frente al tiempo para cualquier situación: