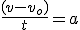Como sabes las matemáticas nos pueden resultar muy útiles para describir los movimientos y predecir dónde se encontrará un determinado móvil pasado un tiempo, por ejemplo. Vamos a deducir las ecuaciones que describen la posición y la velocidad de un MRUA. A diferencia del MRU ahora tenemos que usar dos ecuaciones porque ya no sólo varía la posición sino que también cambia la velocidad. Para deducirlas vamos a trabajar con el siguiente simulador que ya te debe resultar familiar.

Vamos a simular un movimiento con aceleración constante. Para ello vamos a fijar una posición inicial, por ejemplo 40 m a la izquierda del origen de nuestro sistema de referencia, y una velocidad inicial. Supongamos por ejemplo que nuestro móvil se mueve con una velocidad de 5 m/s. Finalmente, y esto es una novedad respecto al MRU, vamos a dar un valor distinto de cero a la aceleración. Por ejemplo vamos a establecerla en 2 m/s².

Una vez fijados estos parámetros pulsa sobre "Comenzar" y observa el movimiento.

Como has podido observar nuestro móvil se desplaza cada vez con mayor rapidez. Vamos a analizar los datos de la tabla.

Observando la tabla vemos que se han anotado tanto la posición de nuestro móvil, medida en metros, como su velocidad, medida en metros por segundo, desde el instante 0 segundos hasta el instante 10 segundos con intervalos de 1 segundo de separación.

Si nos fijamos en cómo va cambiando la velocidad encontramos que cada segundo que pasa, esta crece en 2 unidades. Esto es coherente con el valor de la aceleración que hemos marcado en el simulador.

Si calculamos la aceleración en cualquier intervalo el valor siempre será 2 metros por segundo al cuadrado.

¿Podríamos encontrar una ecuación que nos diera el valor de la velocidad v en cualquier instante t? Sí, y además resulta muy sencillo.

En este caso la aceleración es constante y como sabemos por su definición que:

La aceleración y la velocidad inicial tomarán cada una un valor constante y normalmente el instante inicial será 0 segundos. Despejando de la anterior ecuación y llamando v_o a la velocidad inicial tendremos que:

Con esta ecuación podemos determinar la velocidad en cualquier instante conociendo la velocidad inicial y la aceleración. En nuestro ejemplo tendríamos que la ecuación general:

queda así al sustituir los valores de la aceleración y la velocidad inicial y teniendo en cuenta que empezamos a medir el tiempo justo cuando empieza a moverse nuestro objeto (to=0s),