2.2. Cicloide
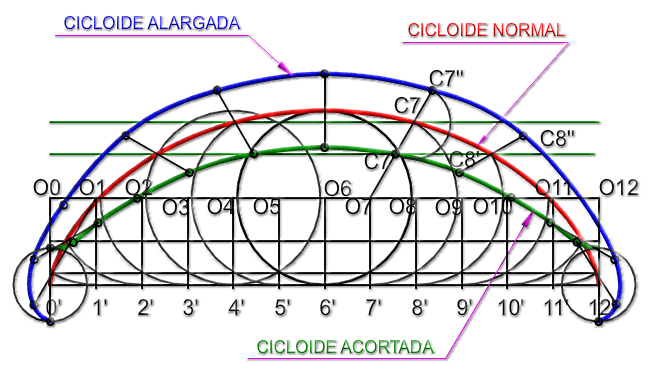
- Normal: el punto generador está contenido en la circunferencia ruleta.
- Acortada: el punto generador está contenido en el radio de la circunferencia ruleta a una distancia menor (punto interior).
- Alargada: el punto generador está contenido en el radio de la circunferencia ruleta a una distancia mayor (punto exterior)
En la imagen superior puedes ver los tres tipos.
Para la notación de los puntos de las cicloides que vamos a determinar usaremos la letra C, quedando de la siguiente manera:
- Normal: C.
- Acortada: C'
- Alargada: C''.
TRAZADO.
El dato inicial es el diámetro de la circunferencia ruleta, a partir de él obtenemos mediante su rectificación y división, los puntos de la cicloide.
Recuerda que el número de divisiones de la circunferencia, nosotros recomendamos doce (12), está relacionado con los puntos que obtengas para el posterior trazado de la curva.
- Normal.
En la siguiente animación puedes ver cómo se dibuja este tipo de cicloide.
-
Acortada.
Para poder dibujarla debemos partir de la disposición de los puntos de una cicloide normal, no tienes que trazar la curva, la distancia que se recorta puede ser cualquiera, para facilitar el trazado te recomendamos que uses una magnitud de fácil manejo.
En la animación inferior te mostramos el trazado de una cicloide acortada, lógicamente hemos omitido parte del trazado de la normal.
Al final de la animación puedes comparar este tipo de cicloide con la normal.
- Alargada.
Como en el caso anterior, en el trazado de este tipo de curvas es preciso situar los puntos de una cicloide normal y determinar la magnitud de alargue del radio de la ruleta, de manera que te permita un dibujo cómodo.
En la siguiente animación puedes ver su trazado, en este caso también hemos suprimido parte del trazado de la normal.
Al final puedes comparar la cicloide alargada con la normal.
Curvas trigonométricas, gráfica del seno.
Son la representación gráfica de funciones trigonométricas: seno, coseno y tangente.
Su dibujo está basado en el trazado de la cicloide, ya que partimos de la división y rectificación de una circunferencia generatriz.
Para representar este tipo de curvas recurrimos a un sistema cartesiano (ejes x, y).
En la siguiente animación puedes ver cómo se representa la gráfica del seno, denominada también senoide o sinusoide.
En el siguiente vídeo puedes ver las propiedades de la cicloide, este experimento ha sido realizado y filmado en el IES Historiador Chabàs de Dénia por los profesores Juan Bragado, Jose Luis Ronda y Juan Luis López en presencia de alumnos de los cursos 3º ESOD y 4º ESOC el 13 de Mayo de 2011.
|
|
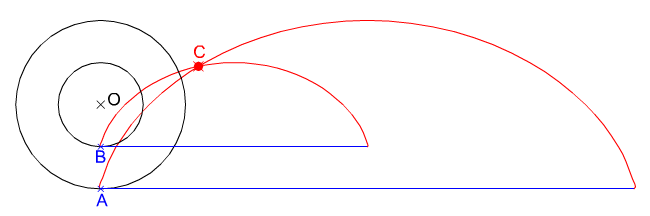
| En la imagen superior puedes ver el punto intersección (C) de las cicloides de dos circunferencias concéntricas. Te pedimos que determines dicho punto C sabiendo que los radios de las circunferencias son: OA = 30 mm y OB = 15 mm. Para resolverlo debes de aplicar el método explicado para dibujar la cicloide normal. Material necesario:
|
| Este ejercicio debes realizarlo en una hoja formato A4. |