1.1. Propiedades y clasificación
PROPIEDADES.
Una curva cíclica es el lugar geométrico de un punto que está relacionado con una circunferencia o recta (siempre se encuentra en la misma posición respecto a ésta), que rueda si resbalar sobre otra circunferencia o recta.
La línea que genera este punto en movimiento está formada por las infinitas posiciones de este punto móvil.
Elementos.
En las curvas cíclicas intervienen dos elementos, tangentes entre sí:
- Ruleta: elemento móvil, puede ser una recta o una circunferencia.
- Directriz: elemento fijo, el camino sobre el que rueda la ruleta. Puede ser una recta o una circunferencia.
En la animación inferior puedes ver cómo se genera una cicloide, su ruleta es una circunferencia tangente a una recta directriz.
- Si la ruleta es circular podrá ser exterior o interior a la base según donde se produzca el rodamiento.
- Si la ruleta es una recta será siempre exterior.
CLASIFICACIÓN.
Atendiendo a la tangencia entre la ruleta y la directriz podemos clasificar a las curvas cíclicas en dos grupos:
- Tangencia entre circunferencia y recta.
- Tangencia entre circunferencias.
En la siguiente animación puedes ver dicha clasificación así como los elementos de las curvas.
Epicicloide e Hipocicloide, cálculo del ángulo de la circunferencia directriz.
El ángulo central que delimita el desarrollo de la ruleta se determina aplicando la fórmula:
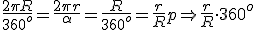
Ejemplo: ángulo central de una epicicloide, radio de la ruleta 30 mm, radio de la directriz 90 mm.
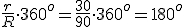
Si quieres calcular el ángulo del arco directriz puedes usar la siguiente aplicación:
Introduce el radio de la RULETA:
Introduce el radio de la DIRECTRIZ:
Ángulo central: o (centesimal)
