2.2. Entre circunferencias
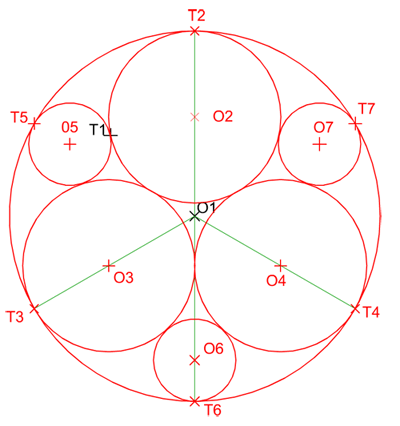
Recuerda que cuando dos circunferencias son tangentes entre sí sus centros están alineados con el punto de tangencia.
ENTRE DOS CIRCUNFERENCIAS:
- Conocido el radio y el punto de tangencia: dos posibilidades una interior y otra exterior. Se resuelve aplicando las propiedades segunda y cuarta de las tangencias entre circunferencias.
- Conocido el punto de tangencia y que pase por un punto exterior: se resuelve aplicando las propiedades primera, segunda y cuarta de las tangencias entre circunferencias.
ENTRE CIRCUNFERENCIAS: dos posibilidades una interior y otra exterior.
- Circunferencias tangentes a tres dadas de igual centro: las tres rectas configuran un triángulo, por tanto, este problema se resuelve determinando su circuncentro.
- Circunferencias tangentes a dos dadas conocido el punto de tangencia en una de ellas: se resuelve aplicado homotecia.
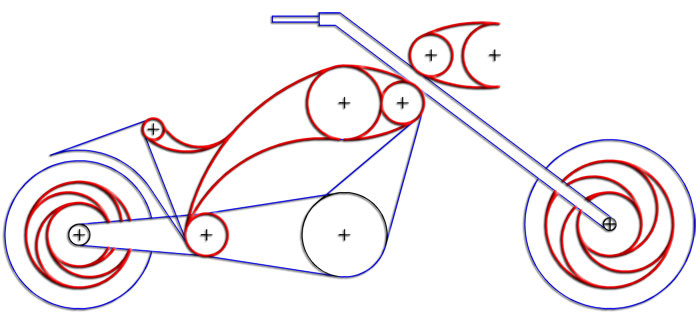
 Dibuja la pieza representada en la imagen izquierda, usando esta plantilla, empleando los conceptos y procedimientos de las tangencias
entre circunferencias.
Dibuja la pieza representada en la imagen izquierda, usando esta plantilla, empleando los conceptos y procedimientos de las tangencias
entre circunferencias.
¿Necesitas ayuda para resolver este ejercicio?